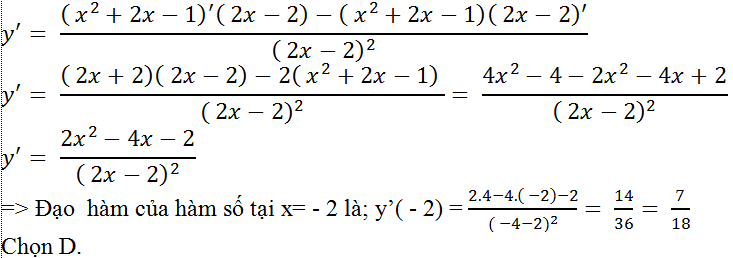[Tìm hiểu] công thức tính nhanh đạo hàm của các hàm số cơ bản

[ Tìm hiểu ] công thức tính nhanh đạo hàm của những hàm số cơ bản

Các công thức đạo hàm là phần kiến thức và kỹ năng Toán 11 rất quan trọng nhưng lại nhiều và khá phức tạp. Nếu không được rèn luyện liên tục học viên sẽ thuận tiện quên ngay. Bài viết ngày hôm nay, THPT Sóc Trăng sẽ mạng lưới hệ thống lại khá đầy đủ và chi tiết cụ thể công thức tính nhanh đạo hàm và nhiều dạng bài tập thường gặp. Các bạn xem để lưu lại nhé !

I. LÝ THUYẾT CHUNG

Bạn đang đọc: [Tìm hiểu] công thức tính nhanh đạo hàm của các hàm số cơ bản – Trường THPT Thành Phố Sóc Trăng

1. Đạo hàm là gì ?

Bạn đang xem : [ Tìm hiểu ] công thức tính nhanh đạo hàm của những hàm số cơ bản
Trong giải tích toán học, đạo hàm của một hàm số thực ra là sự miêu tả sự biến thiên của hàm số tại một điểm nào đó .
Trong vật lý, đạo hàm màn biểu diễn tốc độ tức thời của một điểm hoạt động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn .
Trong hình học đạo hàm là thông số góc của tiếp tuyến với đồ thị trình diễn hàm số. Tiếp tuyến đó là xê dịch tuyến tính gần đúng nhất của hàm ở gần giá trị nguồn vào .

2. Đạo hàm của các hàm số lượng giác là gì?

Đạo hàm của những hàm lượng giác là chiêu thức toán học tìm vận tốc biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin ( x ), cos ( x ) và tan ( x ) .

II. CÔNG THỨC TÍNH NHANH ĐẠO HÀM CỦA CÁC HÀM SỐ THƯỜNG GẶP

1. Đạo hàm của hàm phân thức

Để tính đạo hàm phân thức ta sử dụng chung một công thức

$left( {frac{u}{v}} right)' = frac{{u'.v - v'.u}}{{{v^2}}}$

Công thức đặc biệt: $left( {frac{1}{x}} right)' = frac{{ - 1}}{{{x^2}}};left( {frac{1}{u}} right)' = - frac{{u'}}{{{u^2}}}$

2. Đạo hàm của hàm phân thức bậc 1/ bậc 1

$y = frac{{ax + b}}{{cx + d}} Rightarrow y' = frac{{ad - bc}}{{{{left( {cx + d} right)}^2}}}$

Ví dụ: Tính đạo hàm của hàm số:

Hướng dẫn giải

a. $y' = frac{{3.left( { - 1} right) - left( { - 2} right).1}}{{{{left( {x - 1} right)}^2}}} = frac{{ - 1}}{{{{left( {x - 1} right)}^2}}}$

b. $y' = frac{{1.3 - 5.2}}{{{{left( {2x + 3} right)}^2}}} = frac{{ - 7}}{{{{left( {2x + 3} right)}^2}}}$

3. Đạo hàm của hàm phân thức bậc 2/ bậc 1

$y = frac{{a{x^2} + bx + c}}{{dx + e}} Rightarrow y' = frac{{ad{x^2} + 2aex + be - cd}}{{{{left( {dx + e} right)}^2}}}$

Ví dụ: Tính đạo hàm của hàm số $y = frac{{3{x^2} - 2x + 1}}{{x + 2}}$

Hướng dẫn giải

$y = frac{{3{x^2} - 2x + 1}}{{x + 2}} Rightarrow y' = frac{{3.1{x^2} + 2.3.2x + left( { - 2} right).2 - 1.1}}{{{{left( {x + 2} right)}^2}}} = frac{{3{x^2} + 12x - 5}}{{{{left( {x + 2} right)}^2}}}$

4. Đạo hàm của hàm phân thức bậc 2/ bậc 2

$begin{matrix} y = dfrac{{{a_1}{x^2} + {b_1}x + {c_1}}}{{{a_2}{x^2} + {b_2}x + {c_2}}} Rightarrow y' = dfrac{{left| {begin{array}{*{20}{c}} {{a_1}}&{{b_1}} \ {{a_2}}&{{b_2}} end{array}} right|{x^2} + 2left| {begin{array}{*{20}{c}} {{a_1}}&{{c_1}} \ {{a_2}}&{{c_2}} end{array}} right|x + left| {begin{array}{*{20}{c}} {{b_1}}&{{c_1}} \ {{b_2}}&{{c_2}} end{array}} right|}}{{{{left( {{a_2}{x^2} + {b_2}x + {c_2}} right)}^2}}} hfill \ Rightarrow y' = dfrac{{left( {{a_1}{b_2} - {a_2}{b_1}} right){x^2} + 2left( {{a_1}{c_2} - {a_2}{c_1}} right)x + {b_1}{c_2} - {b_2}{c_1}}}{{{{left( {{a_2}{x^2} + {b_2}x + {c_2}} right)}^2}}} hfill \ end{matrix}$

Ví dụ: Tính đạo hàm của hàm số $y = frac{{3{x^2} - 2x + 1}}{{{x^2} + x + 2}}$

Hướng dẫn giải

$y = frac{{3{x^2} - 2x + 1}}{{{x^2} + x + 2}} Rightarrow y' = frac{{left| {begin{array}{*{20}{c}} 3&{ - 2} \ 1&1 end{array}} right| + 2left| {begin{array}{*{20}{c}} 3&1 \ 1&2 end{array}} right|x + left| {begin{array}{*{20}{c}} { - 2}&1 \ 1&2 end{array}} right|}}{{{{left( {{x^2} + x + 2} right)}^2}}} = frac{{5{x^2} + 10x - 5}}{{{{left( {{x^2} + x + 2} right)}^2}}}$

5. Công thức tính nhanh đạo hàm của một số hàm số thường gặp

Hàm số bậc nhất / bậc nhất : f ( x ) = ax + b / cx + d ⇒ f ′ ( x ) = ad − bc / ( cx + d ) 2 .
Hàm số bậc hai / bậc nhất : f ( x ) = ax2 + bx + c / mx + n ⇒ f ( x ) = amx2 + 2 anx + bn − cm / ( mx + n ) 2
Hàm số đa thức bậc ba : f ( x ) = ax3 + bx2 + cx + d ⇒ f ( x ) = 3 ax2 + 2 bx + c
Hàm số trùng phương : f ( x ) = ax4 + bx2 + c ⇒ f ′ ( x ) = 4 ax3 + 2 bx .
Hàm số chứa căn bậc hai : f ( x ) = √ u ( x ) ⇒ f ′ ( x ) = u ′ ( x ) / 2 √ u ( x )
Hàm số chứa trị tuyệt đối : f ( x ) = | u ( x ) | ⇒ f ′ ( x ) = u ′ ( x ). u ( x ) / | u ( x ) | .

III. QUY TẮC TÍNH NHANH ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC

Các hàm số u = u ( x ), v = v ( x ), w = w ( x ) có đạo hàm, khi đó .
( u + v ) ’ x = u ’ + v ’ ; ( u-v ) ’ = u ’ – v ’ ; ( ku ’ ) = k. u ’, k ∈ R .
( uv ) ’ = u’v + u. v ’ ; ( u / v ) ’ = ( u’v – uv ’ ) / v²
Đạo hàm những hàm số lượng giác lớp 11 .
( sinx ) ’ = cosx
( cosx ) ’ = – sinx
( tanx ) ’ = 1 / cos²x = 1 + tan²x ( x ≠ π / 2 + kπ, k ∈ Z ) .

(cotx)’ = -1/sin²x = -(1 +cot²x).

Xem thêm: Làm cách nào để xem video trên Google Drive đã bị hết lượt xem?

( x ≠ π, k ∈ Z ) .
( Sinu ) ’ = cosu. u ’ .
( cosu ) ’ = – sinu. u ’ .
( tanu ’ ) = u ’ / cos²u = ( 1 + tan²u ) u ’ ( u ≠ π / 2 + kπ, k ∈ Z ) .
( cotu ) ’ = – u ’ / sin²x = – 1 ( 1 + cot²u ) u ’ ( u ≠ kπ, k ∈ Z ) .
Trên đây là một số ít quy tắc tính đạo mà những em cần phải nhớ. Chỉ khi nắm vững được phần kỹ năng và kiến thức này những em mới hoàn toàn có thể thuận tiện giải được những bài toán xét tính đơn điêu, tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác …

IV. BÀI TẬP TÍNH ĐẠO HÀM CỦA CÁC HÀM SỐ LƯỢNG GIÁC

Bài 1:

Đạo hàm của hàm số y = 1 / ( cos²x – sin²x ) là :
A. y ’ = 2 sin2x / cos²2x B. y ’ = 2 cos2x / cos²2x
C. y ’ = cos2x / cos²2x D. y ’ = sin2x / cos²2x .
Hướng dẫn giải :
y = 1 / ( cos²x – sin²x ) = 1 / cos2x .
Áp dụng quy tắc tính đạo hàm với ( 1 / u ) ’ = – u ’ / u² ta được ”
y ’ = – ( cos2x ) ’ / ( cos2x ) ² = sin2x. ( 2 x ) ’ / cos²2x = 2 sin2x. cos²2x .

Bài 2:

Cho hàm y = cotx / 2. Hệ thức nào sau đây là đúng ?
A. y² + 2 y ’ = 0 B. y² + 2 y ’ + 1 = 0
C. y² + 2 y ’ + 2 = 0 D. y² + 2 y ’ – 1 = 0 .
Hướng dẫn giải :
Ta có y ’ = – 1 / ( sin²x / 2 ) = – 50% ( 1 + cot²x / 2 ) .
Do đó y² + 2 y ’ = cot²x / 2 – 2.1 / 2 ( 1 + cot²x / 2 ) = cot²x / 2 – ( 1 + cot²x / 2 ) = – 1 nên y² + 2 y ’ + 1 = 0. Chọn đáp án B .
Cách 2 : Sử dụng máy tính casio .
Bước 1 : Thiết lập môi trường tự nhiên SHIFT MODE 4 .
Thay x = 1 vào y = cotx / 2 ta tính được y cot 1/2 ≈ 1
Sử dụng phím SHIFT ∫, nhập hàm số y = cotx / 2 với x = 1 được hiệu quả ≈ – 1 .
Do đó y² + 2 y ’ + 1 = 0 .

Bài 3:

ính đạo hàm cấp n của hàm số y = cos2x là :
A. y ( n ) = ( – 1 ) ncos ( 2 x + n π / 2 )
B. y ( n ) = 2 n cos ( 2 x + π / 2 ) .
C. y ( n ) = 2 n + 1 cos ( 2 x + nπ / 2 ) .
D. y ( n ) = 2 n cos ( 2 x + nπ / 2 ) .
Hướng dẫn giải :
Ta có y ′ = 2 cos ( 2 x + π2 ), y ′ ′ = 2 ²cos ( 2 x + 2 π2 )
y ′ ′ ′ = 2 ³cos ( 2 x + 3 π2 )
Bằng quy nạp ta chứng tỏ được y ( n ) = 2 ncos ( 2 x + nπ2 )

Bài 4:

Cho hàm số y = ( x2 + 2 x – 1 ) / ( 2 x – 2 ). Tính đạo hàm của hàm số tại x = – 2