1. Lũy thừa với số mũ nguyên
Cho a ∈ ℝ, n ∈ ℕ*. Khi đó: ![]()
2. Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
Cho a ≠ 0, n ∈ ℕ*, quy ước:
Bạn đang đọc: Công thức lũy thừa: Tổng hợp công thức chi tiết
Chú ý :00 và 0 – n không có nghĩaNgười ta thường dùng những lũy thừa của 10 với số mũ nguyên để bộc lộ những số rất lớn và những số rất bé. Chẳng hạn : Khối lượng của Trái Đất là 5,97. 1024 kg ; khối lượng nguyên tử của hiđrô là 1,66. 10-24 kg .
3. Căn bậc n
Khái niệmCho số thực b và số nguyên dương n ≥ 2. Số a được gọi là căn bậc n của số b nếu an = b
Khi n lẻ và b ∈ ℝ: Tồn tại duy nhất căn bậc n của b, kí hiệu
Khi n chẵn :b < 0 : Không sống sót căn bậc n của b
b = 0: Có một căn bậc n của b, kí hiệu
b > 0 : Có hai căn bậc n của b trái dấu, kí hiệu giá trị dương là, còn giá trị âm là , còn giá trị âm làTính chất của căn bậc nVới hai số không âm a, b ; hai số nguyên dương m, n ta có :
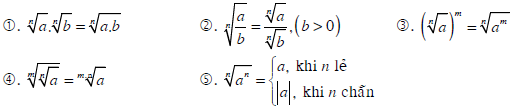
Lũy thừa với số mũ hữu tỉ
Cho số thực a > 0 và số hữu tỉ
, trong đó m ∈ ℤ, n ∈ ℕ, n ≥ 2., trong đó m ∈ ℤ, n ∈ ℕ, n ≥ 2 .
Lũy thừa của a với số mũ r là số ar xác định bởi:
Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, α là một số vô tỉ và (rn) là một dãy số hữu tỉ sao cho
Khi đó:
Tính chất của lũy thừa với số mũ thựcCho a, b là những số thực dương ; α, β là những số thực tùy ý. Khi đó, ta có :
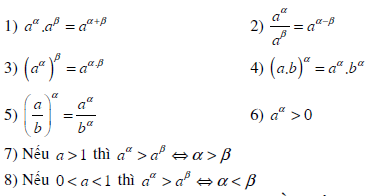
Bài tập vận dụng công thức lũy thừa
Dạng 1. Tính các giá trị của một biểu thức – Rút gọn biểu thức.
Bài 1. Tính các biểu thức sau:
Hướng dẫn giải
Bài 2. Tính các biểu thức sau:
Hướng dẫn giải
Bài 3. Tính các biểu thức sau:
Hướng dẫn giải
Bài 4. Tính các biểu thức sau:
Hướng dẫn giải
Bài 5. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Bài 6. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Bài 7. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Dạng 2. Chứng minh đẳng thức, bất đẳng thức – So sánh giá trị của biểu thức
Chú ý :Nếu a > 1 thì α < β ⇔ aα < aβNếu 0 < a < 1 thì α < β ⇔ aα > aβ
Bài 1. Hãy so sánh các cặp số sau:
Hướng dẫn giải
a) Ta có
Do 12 < 18 nên
Vì cơ số a = 5 > 1 nên
b) Ta có
c) Ta có
d) Ta có
Bài 2. Hãy so sánh các cặp số sau:
Hướng dẫn giảia ) Đưa hai căn đã cho về cùng căn bậc 15, ta được :
Do 100000 > 8000 nên
b) Ta có
Do 125 < 2401 nên
c) Ta có
Do 371293 > 279841 nên
d) Ta có
Bài 3. Hãy so sánh các cặp số sau:
Hướng dẫn giải
a) Ta có
Do 8 < 9 nên
b) Ta có
c) Ta có
d) Ta có
Bài 4. Không dùng máy tính và bảng số. Chứng minh:
Hướng dẫn giải
a)
Cách 1. Ta có:
.
Tương tự:
Suy ra:
Cách 2. Đặt
. Ta cần chứng minh x = 2. Ta cần chứng tỏ x = 2Ta có :
Từ đó ta có : x3 + 3 x – 14 = 0 ⇔ ( x – 2 ) ( x2 + 2 x + 7 ) = 0 ⇔ x = 2 ( vì x2 + 2 x + 7 > 0 )
Cách 3. Ta có:
. Do đó nếu và
là nghiệm của phương trình X2 – 2X – 1 = 0, tức là:
. Do đónếuvàlà nghiệm của phương trình X – 2X – 1 = 0, tức là :
Ta chứng minh đẳng thức (1). Ta có:
. Từ đó suy ra (1).. Từ đó suy ra ( 1 ) .Đẳng thức ( 2 ) chứng tỏ tựa như. Từ ( 1 ) và ( 2 ) suy ra điều phải chứng tỏ .
b)
Đặt
. Ta cần chứng minh x = 3. Ta cần chứng tỏ x = 3Ta có :
⇔ x3 – 5 x – 12 = 0 ⇔ ( x – 3 ) ( x2 + 3 x + 4 ) = 0 ⇔ x = 3 ( vì x2 + 3 x + 4 > 0 )
c)
Cách 1. Ta có :
Vì
nên nênCách 2. Ta có :
Nên
d)
Có thể giải bằng ba cách như câu a )Đặt H68. Ta cần chứng tỏ x = 3
Ta có:
⇔ x3 – 3x – 18 = 0⇔ x – 3 x – 18 = 0⇔ ( x – 3 ) ( x2 + 3 x + 6 ) = 0 ⇔ x = 3 ( vì x2 + 3 x + 6 > 0 )
Bài tập tự luyện
Bài 1. Hãy tính:
Bài 2. Đơn giản các biểu thức sau:
Bài 3. Đơn giản các biểu thức sau:
Bài 4. Đơn giản các biểu thức sau:
Bài 5. So sánh các số:
Bài 6. Chứng minh rằng: 
Bài 7. Rút gọn các biểu thức sau:
Kết quả :Bài 1
Bài 2
Bài 4
Bài 5
Bài 7
Thầy Dũng dạy toán học từ năm 2010 sau khi nhận bằng sư phạm môn toán tại trường Đại Học Sư Phạm Đà Nẵng. Triết lý dạy học của thầy luôn coi trọng chất lượng hơn số lượng bởi ở một góc nhìn nào đó, tất cả chúng ta sử dụng toán học hằng ngày trong đời sống và cần phải hiểu rõ về thực chất của nó thay vì học sơ sài. Thầy cảm xúc rất như mong muốn khi được làm biên tập viên cho môn toán tại VerbaLearn, nơi mà những bài dạy của thầy hoàn toàn có thể tiếp cận nhiều học viên hơn .
Source: https://taimienphi.club
Category: Chưa phân loại
