Bảng Công Thức Logarit Bản Đầy Đủ| www.https://taimienphi.club

Trong loạt series chia sẽ kiến thức từ Trung Tâm Gia Sư Trí Việt, bài viết hôm nay chúng tôi sẽ chia sẽ kiến thức toán cơ bản về hàm mũ và logarit. Nhằm giúp bạn đọc hiểu thêm về các công thức tính hàm mũ và logarit.

Trong toán học, logarit là phép toán nghịch đảo của lũy thừa. Điều đó có nghĩa logarit của một số là số mũ của một giá trị cố định, gọi là cơ số, phải được nâng lên lũy thừa để tạo ra con số đó. Trong trường hợp đơn giản logarit là đếm số lần lặp đi lặp lại của phép nhân. Ví dụ, logarit cơ số 10 của 1000 là 3, vì 10 mũ 3 là 1000 (1000 = 10 × 10 × 10 = 103); phép nhân được lặp đi lặp lại ba lần. Tổng quát hơn, lũy thừa cho phép bất kỳ số thực dương nào có thể nâng lên lũy thừa với số mũ thực bất kỳ, luôn luôn tạo ra một kết quả là số dương, vì vậy logarit có thể được tính toán cho bất kỳ hai số dương thực a và b trong đó a≠1.

Định Nghĩa Logarit

Cho hai số dương a và b với a≠1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.

\alpha =\log _{a}b\Leftrightarrow a^{\alpha }=b

John Napier là người phát minh ra logarit. Thuật ngữ “logarit” do ông đề nghị xuất phát từ sụ kết hợp hai từ Hy Lạp λόγoς (đọc là “logos” có nghĩa là tỉ số) và ‘αρiθμ ός (đọc là “aritmos” nghĩa là số)

Bạn đang đọc: Bảng Công Thức Logarit Bản Đầy Đủ| www.https://taimienphi.club

Quy tắc tính logarit

logarit của một tích

Cho ba số dương a, b, c với a ≠ 1, ta có:

\log _{a}(bc)=\log _{a}b+\log _{a}c

Nhờ quy tắc này mà nhiều thế kỷ trước những nhà toán học và kỹ thuật hoàn toàn có thể sử dụng bảng logarit để triển khai phép nhân hai số trải qua phép cộng logarit, do phép cộng thì dễ tính hơn phép nhân. Nhà toán học John Napier đã ý tưởng ra phép tính này ở thế kỷ 17 .

Để sử dụng bảng logarit, người ta thường đưa về logarit cơ số a = 10, gọi là logarit thập phân để thuận tiện cho tra bảng và tính toán. logarit tự nhiên lấy hằng số e (xấp xỉ bằng 2,718) làm cơ số, và nó được sử dụng rộng rãi trong toán thuần túy. Logarit nhị phân với cơ số bằng 2 được sử dụng trong khoa học máy tính.

Thang logarit được cho phép thu hẹp những đại lượng về khoanh vùng phạm vi nhỏ hơn. Ví dụ, độ Richter đo nguồn năng lượng của động đất cũng sử dụng thang đo logarit, savart là đơn vị chức năng logarit đo cao độ âm thanh, decibel là đơn vị chức năng logarit đo áp suất âm thanh. logarit cũng thường gặp trong những công thức khoa học và kỹ thuật, như đo độ phức tạp của thuật toán và fractal, thậm chí còn trong công thức đếm số nguyên tố .

logarit của một lũy thừa

Cho hai số dương a, b; với a ≠ 1. Với mọi α ta có: logabα = αlogab

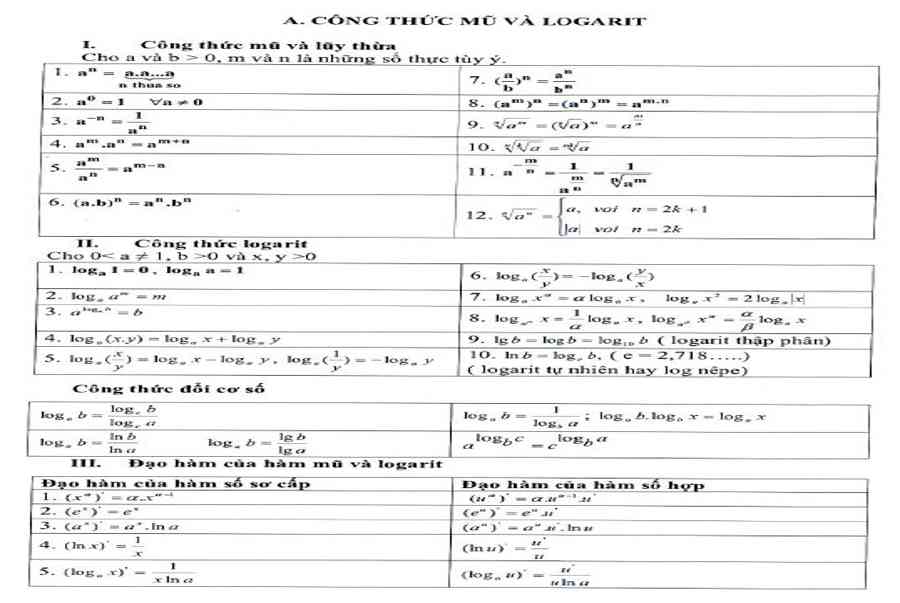
Xem bảng tổng hợp công thức mũ và logarit tại đây :

Chuyên đề công thức logarit là một trong những câu hỏi dễ kiếm điểm, chính vì thế mà bạn cần lấy điểm tuyệt đối ở chuyên đề này. Để mạng lưới hệ thống và ôn luyện kỹ năng và kiến thức giúp bạn hoàn toàn có thể có 1 kỳ thi ĐH đạt tác dụng cao, bạn cũng hoàn toàn có thể tìm hiểu thêm dịch vụ gia sư luyện thi ĐH ở phía dưới :

Xem video công thức logarit tại đây :

Nâng cao kỹ năng và kiến thức giải toán trắc nghiệm 100 % dạng bài mũ – logarit, số phức – Tô Thị Nga

Nội dung sách:
Chuyên đề 1. Mũ – Logarit
Vấn đề 1. Lũy thừa – Mũ – Logarit
+ Chủ đề 1. Lũy thừa – Logarit
+ Chủ đề 2. Hàm số mũ và hàm số logarit
Vấn đề 2. Phương trình mũ và logarit
Vấn đề 3. Bất phương trình mũ và logarit
1. Phương pháp đưa về cùng cơ số
2. Phương pháp mũ hóa, logarit hóa
3. Phương pháp đặt ẩn phụ
4. Giải bất phương trình mũ – logarit bằng phương pháp hàm số
5. Giải bất phương trình mũ – logarit bằng phương pháp đánh giá – bất đẳng thức
Vấn đề 4. Hệ phương trình và hệ bất phương trình mũ – logarit
+ Dạng 1. Giải hệ mũ – logarit bằng phương pháp biến đổi tương đương
+ Dạng 2. Giải hệ mũ – logarit bằng cách đặt ẩn phụ
+ Dạng 3. Giải hệ mũ – logarit bằng phương pháp hàm số
+ Dạng 4. Giải hệ mũ – logarit bằng phương pháp đánh giá bất đẳng thức
Chuyên đề 2. Số phức
Vấn đề 1. Số phức
Vấn đề 2. Các bài toán về biểu diễn hình học của số phức
Vấn đề 3. Tìm số phức có mô-đun lớn nhất, nhỏ nhất
Vấn đề 4. Căn bậc hai của số phức và phương trình căn bậc hai – Các phương trình quy về bậc hai – Hệ phương trình
Vấn đề 5. Dạng lượng giác của số phức

XEM TÀI LIỆU ONLINE