Bamboo đoán rằng bạn đang gặp phải và đắn đo rất lớn về 2 yếu tố đúng không nào ? Thứ nhất, bạn không nắm vững kỹ năng và kiến thức cơ bản về công thức cấp số cộng và công thức cấp số nhân. Thứ hai, bạn vẫn muốn tìm cách giải nhanh những công thức cấp số cộng và cấp số nhân nhưng chưa biết tìm cách nào để giải .
Sau đây là cách mà Bamboo gợi ý để bạn mạng lưới hệ thống lại kiến thức và kỹ năng và thực hành thực tế :
- Xem lại các phần quan trọng trong lý thuyết như định nghĩa, tính chất của cấp số cộng và cấp số nhân.
- Xem thật kỹ và ghi nhớ công thức giải nhanh mà Bamboo sắp giới thiệu sau đây.
- Nghiền ngẫm thật chi tiết và cẩn thận về các ví dụ đính kèm lời giải.
Cấp số cộng và cấp số nhân – những lý thuyết khá là “khó nhằn” với môn toán 11. Sau đây, hãy để Bamboo giới thiệu những công thức cấp số cộng và công thức cấp số nhân kèm bài tập vận dụng.
Cấp số cộng là gì?
- (un) là cấp số cộng với công sai d thì: un + 1 = un + d
- Nếu un+1 – un là hằng số d với mọi n ϵ N* thì (un) là cấp số cộng có công sai d.
- Nếu un+1 – un còn phụ thuộc vào n thì (un) không là cấp số cộng.
- Công thức số hạng tổng quát: Un = U1 + ( n − 1 ) d, với n ≥ 2
- Tính chất: un
= \ ( \ frac { u_ { k-1 } + u_ { k + 1 } } { 2 } \ )
với k ≥ 2
Đặc biệt a, b, c là cấp số cộng ⇔ a + c = 2 b
- Tổng của n số hạng đầu của một cấp số cộng:
Sn = U1+U2+…+UnSn=U1+U2+…+Un = \( \frac{n\left(u_1+u_n\right)}{2} \), n ≥ 1 = n.u1 + \( \frac{n\left(n-1\right)}{2} \)d, n ≥ 2

Định nghĩa
Trong Toán học, cấp số cộng là một dãy số mà trong đó, kể từ số hạng thứ 2 trở đi đều sẽ là tổng của số hạng đứng trước nó với 1 số ít không đổi khác 0 được gọi là công sai .

Tính chất
-
Un+1 – Un = Un+2 – Un+1
- Nếu như có 3 số bất kì m, n, q lập thành CSC thì 3 số đó luôn thỏa mãn m + q = 2n
- Số hạng tổng quát :
Un = U1 + d(n−1)
- Nếu muốn tính tổng n số hạng đầu, ta có công thức : {\(u=u_1+(n-1)d\); Un= n}
Công thức cấp số cộng
Công thức tính tổng cấp số cộng: ∀n ∈ N*, Un+1 = Un + d
Giải thích :
- Với d được gọi là công sai
- Un+1 – Un = d với mọi n ∈ N* ( trong đó d là hằng số còn Un+1; Un là hai số liên tiếp của dãy số CSC)
- Khi hiệu số Un+1 – Un phụ thuộc vào n thì không thể là cấp số cộng
Một số ví dụ bài tập cấp số cộng chi tiết, dễ hiểu
Tìm công sai d của cấp số cộng
[Trích từ đề thi tham khảo lần 2 – năm 2020] Cho cấp số cộng (un) với u1 = 3, u2 = 9. Tìm công sai của cấp số cộng:
Hướng dẫn giải:
Cấp số cộng Un với số hạng tổng quát Un = U1 + d(n−1)
Với số hạng đầu U1 và công sai d
Từ đó ta có : U2 = U1 + d ⇔ 9 = 3 + d ⇔ d = 6
Vậy, công sai của cấp số cộng là 6 .
Cách tính tổng của cấp số cộng của n số hạng đầu tiên
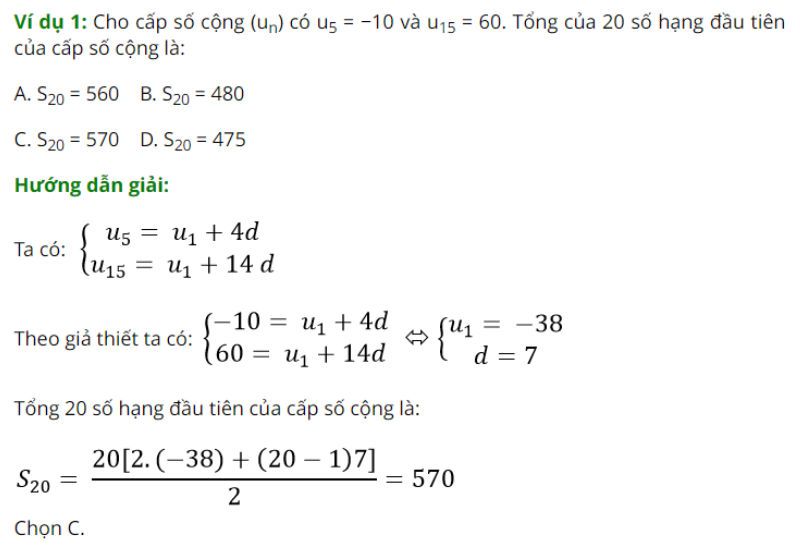
Cấp số nhân là gì?

Định nghĩa
Cấp số nhân là dãy số mà trong đó có số hạng đầu là một số ít khác 0 và kể từ số hạng thứ 2 trở đi đều bằng tích của số hạng đứng liền ngay trước nó với 1 số ít không đổi khác 0 gọi là công bội q .
Tính chất
Nếu ( un ) là một cấp số nhân thì kể từ số hạng thứ hai, bình phương của mỗi số hạng ( trừ số hạng cuối so với cấp số nhân hữu hạn ) bằng tích của hai số hạng đứng kề nó trong dãy, tức là :
U2k = Uk-1. Uk+1
- Số hạng tổng quát: Un=U1.qn−1
- Tổng n số hạng tiên phong :Sn=U1+U2+…+Un
- Tổng của cấp số nhân lùi vô hạn :Với |q| < 1 thì Sn=U1+U2+…+Un
Công thức cấp số nhân
Ta có công thức tổng quát :
Un+1 = Un.q
Trong đó
- n ∈ N*
- Công bội là q
- Hai số liên tiếp trong công bội là Un, Un+1
Một số ví dụ bài tập cấp số nhân chi tiết, dễ hiểu
Tìm công bội q của cấp số nhân
Gợi ý dạng bài tập tìm công bội q của công thức cấp số nhân

Cách tìm các số hạng của cấp số nhân Un
Gợi ý bài tập về các số hạng của cấp số nhân Un

Xem thêm:
Trên đây là một số ít công thức và những dạng bài tập về công thức cấp số cộng và công thức cấp số nhân. Hy vọng về những gì mà Bamboo gợi ý hoàn toàn có thể giúp ích những bạn và tiếp thêm hành trang trong những ngày đi học trên ghế nhà trường .
Source: https://taimienphi.club
Category: Chưa phân loại
