Công thức hình học 12 là tổng hợp của các công thức hình học ở lớp 12, xen lẫn với 1 số công thức cơ bản, cần thiết ta đã được học từ lớp dưới đầy đủ, rõ ràng, dễ hiểu, giúp các em không bị lúng túng khi quên công thức, cũng như nhớ công thức lâu hơn, biết cách vận dụng và làm các bài tập nâng cao, với mức độ phân hóa cao trong đề thi.
TẢI XUỐNG PDF ↓
Tổng hợp công thức hình học 12
Tỉ số góc nhọn trong tam giác vuông: Cho Δ ABC vuông ở A, đường cao AH, góc ACB là góc α.
1. sinα = AB / BC ( ĐỐI chia HUYỀN )
2. cosα = AC / BC ( KỀ chia HUYỀN )
3. tanα = AB / AC ( ĐỐI chia KỀ )
4. cotα = AC / AB ( KỀ chia ĐỐI )
Hệ thức lượng trong tam giác vuông
1. BC² = AB² + AC² ( Định lí Pitago ) => AB² = BC² – AC²
2. AB² = BH.BC
3. AC² = CH.BC
4. AH² = BH.CH
5. AB.AC = BC.AH
6. 1 / AH² = 1 / AB² + 1 / AC²
Định lí côsin
1. a² = b² + c² – 2 bccosA
2. b² = a² + c² – 2 accosB
3. c² = a² + b² – 2 abcosC
Định lí sin
A a / sin A + B / sinB + C / sinC = 2R
Định lí talet
Cho tam giác ABC nhọn, có MN / / BC
a) AM/AB = AN/ AC = MN/ BC
b) AM/MB = AN/ NC
Diện tích trong hình học phẳng
Tam giác thường
a) S = 1/2 AH
b) S = √p(p a)(p b)(p c) (Công thức Hê-rông)
c ) S = pr ( r : bk đ. tròn nội tiếp tam giác )
Tam giác đều cạnh a
a) Đường cao: h = (a√ 3)/2
b) S = (a²√ 3)/4
c) Đường cao cũng là đường trung tuyến, đường phân giác, đường trung trực
Tam giác vuông
a) S = 1/2ab (a, b là 2 cạnh góc vuông)
b) Tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền
Tam giác vuông cân (nửa hình vuông)
a ) S = 1/2. a² ( 2 cạnh góc vuông bằng nhau )
b ) Cạnh huyền bằng a √ 2
Nửa tam giác đều
a ) Là tam giác vuông có một góc bằng 30 º hoặc 60 º
b ) BC = 2AB
c ) AC = a √ 3 / 2
d ) S = a² √ 3 / 8
Tam giác cân
a) S = 1/2 .ah (h: đường cao; a: cạnh đáy)
b ) Đường cao hạ từ đỉnh cũng là đường trung tuyến, đường phân giác, đường trung trực
Hình chữ nhật
S = ab ( a, b là những size )
Hình thoi
S = 1/2 × d1. d2 ( d1, d2 là 2 đường chéo )
Hình vuông
a ) S = a²
b ) Đường chéo bằng a √ 2
Hình bình hành
S = ah ( h : đường cao ; a : cạnh đáy )
Đường tròn
a ) C = 2 πR ( R : nửa đường kính đường tròn )
b ) S = πR² ( R : nửa đường kính đường tròn )
Công thức về các đường trong tam giác và độ dài
Đường trung tuyến
G : là trọng tâm của tam giác
a ) Giao điểm của 3 đường trung tuyến của tam giác gọi là trọng tâm
b ) * BG = 2/3. BN ; * BG = 2GN ; * GN = 1/3. BN
Đường cao
Giao điểm của của 3 đường cao của tam giác gọi là trực tâm
Đường trung trực
Giao điểm của 3 đường trung trực của tam giác là tâm đường tròn ngoại tiếp
tam giác
Đường phân giác
Giao điểm của 3 đường phân giác của tam giác là tâm đường tròn nội tiếp tam
giác
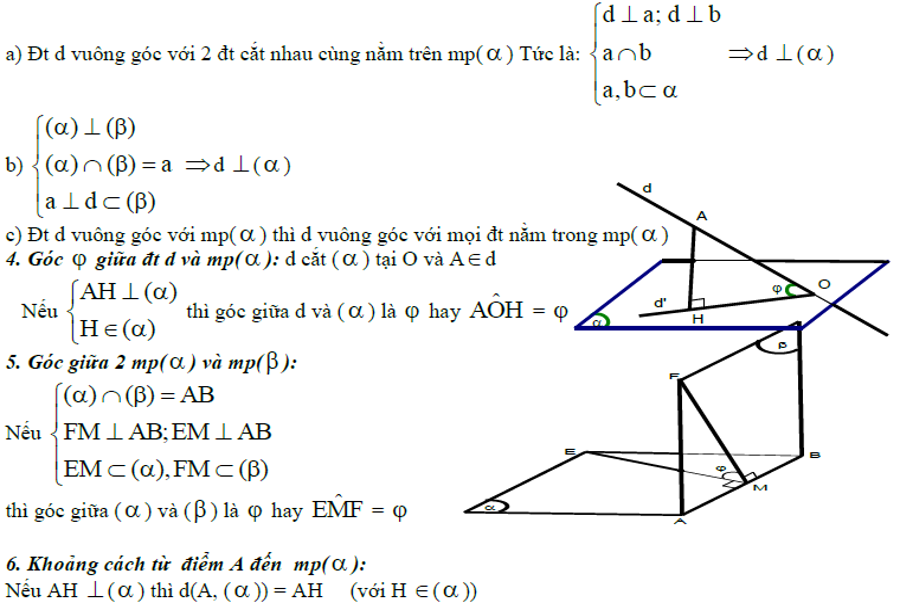
Công thức hình học không gian lớp 12
Hình tứ diện đều
Có 4 mặt là những tam giác đều bằng nhau .
Chân đường cao trùng với tâm của đáy ( hay trùng với trọng tâm của tam giác đáy ) .
Các cạnh bên tạo với mặt dưới những góc bằng nhau
Hình chóp đều
Có đáy là đa giác đều. Có những mặt bên là những tam giác cân đối nhau. Chân đường cao trùng với tâm của đa giác đáy. Các cạnh bên tạo với mặt dưới những góc bằng nhau .
Bảng tóm tắt công thức hình học lớp 12



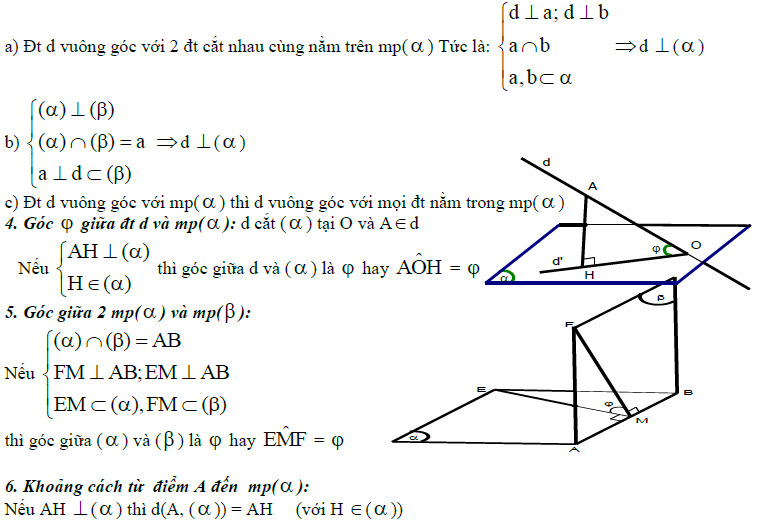
Cảm ơn các em đã xem và tải công thức hình học lớp 12. Chúng tôi mong rằng các công thức này có thể giúp ích các em trong việc tiếp cận toán hình lớp 12 bớt khó khăn hơn, cũng như chuẩn bị tiền đề cho kỳ thi vô cùng quan trọng_ kỳ thi THPT Quốc gia.
Source: https://taimienphi.club
Category: Chưa phân loại