1. Năng lượng từ trường trong ống dây điện

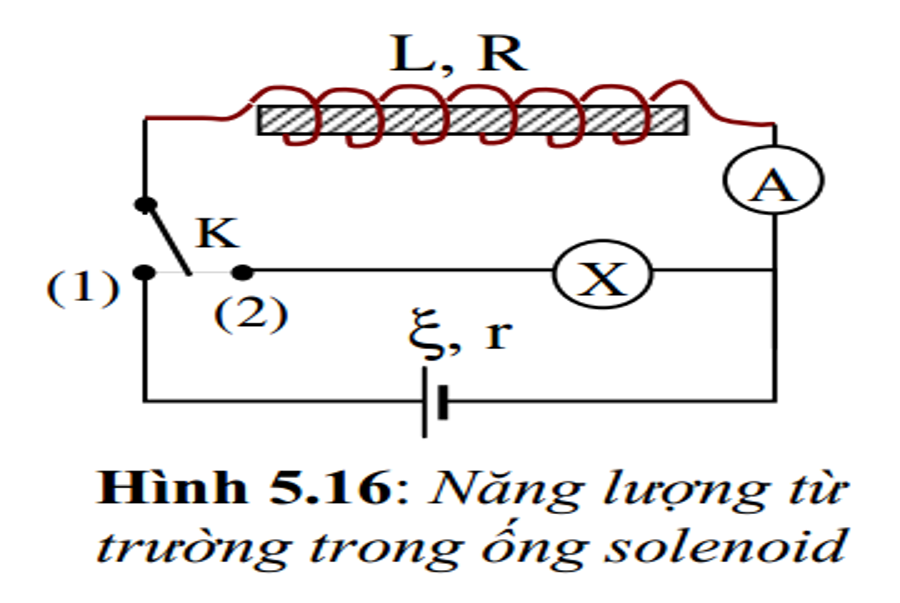
Xét một mạch điện như hình 5.16. Lúc đầu khóa K chưa tiếp xúc với tiếp điểm nào. Trong mạch không có dòng điện .Cho khoa K tiếp xúc với tiếp điểm ( 1 ), có dòng điện chạy qua cuộn dây và số chỉ của ampe kế cho biết dòng điện trong mạch tăng dần từ giá trị không đến giá trị không thay đổi I. Nguyên nhân của hiện tượng kỳ lạ đó là do trong mạch có suất điện động tự cảm chống lại sự tăng của dòng điện, làm cho nó không tăng bất ngờ đột ngột .
Bây giờ ta hãy tính năng lượng mà nguồn điện đã cung cấp cho mạch kể từ lúc đóng khóa K đến khi dòng điện trong mạch đạt giá trị ổn định I.
Bạn đang đọc: Năng lượng từ trường | Vật Lý Đại Cương
Gọi R là điện trở của cuộn dây, r là điện trở nội của nguồn điện, \ ( \ xi \ ) là suất điện động của nguồn điện và \ ( { { \ xi } _ { tc } } \ ) là suất điện động tự cảm sinh ra trong mạch khi dòng điện trong mạch biến thiên. Bỏ qua điện trở những dây nối và điện trở của ampe kế. Tại thời gian t bất kể, cường độ dòng điện trong mạch là i. Theo định luật Ohm mạch kín, ta có :\ ( \ xi + { { \ xi } _ { tc } } = i \ left ( R + r \ right ) \ ) ( 5.19 )Nhân hai vế ( 5.19 ) với idt và thay \ ( { { \ xi } _ { tc } } = – L \ frac { di } { dt } \ ), chuyển vế, ta có :\ ( \ xi idt = { { i } ^ { 2 } } \ left ( R + r \ right ) dt + Lidi \ ) ( 5.20 )Vế trái của ( 5.20 ) chính là năng lượng ( công ) mà nguồn điện đã phân phối cho mạch trong thời hạn dt, ta kí hiệu đại lượng này là dA. Số hạng thứ nhất ở vế phải của ( 5.20 ) là năng lượng nhiệt tỏa ra trong thời hạn dt, ta kí hiệu số hạng này là dQ .Ta có : \ ( dA = dQ = Lidi \ ) ( 5.21 )Lấy tích phân trong khoảng chừng thời hạn từ lúc bắt đầu đến khi dòng điện trong mạch đạt giá trị không thay đổi I, ta được :\ ( A = Q + \ frac { 1 } { 2 } L { { I } ^ { 2 } } \ ) ( 5.22 )( 5.22 ) cho biết, năng lượng mà nguồn điện cung ứng một phần chuyển hóa thành nhiệt và một phần chuyển hóa thành dạng năng lượng khác xác lập bởi biểu thức \ ( \ frac { 1 } { 2 } L { { I } ^ { 2 } } \ ). Năng lượng đó chắc như đinh không phải là những dạng năng lượng quen thuộc như cơ năng, hóa năng, … Vậy nó là năng lượng gì ? Phân tích những đại lượng tương quan đến mạch điện taa thấy, khi có dòng điện Open trong mạch thì có từ trường do dòng điện trong mạch tạo ra. Vì thế buộc ta phải thừa nhận rằng biểu thức \ ( \ frac { 1 } { 2 } L { { I } ^ { 2 } } \ ) chính là năng lượng của từ trường. Với những ống dây điện, từ trường định xứ trong lòng ống dây là hầu hết .
Vậy biểu thức tính năng lượng từ trường của ống dây là: \( {{W}_{m}}=\frac{1}{2}L{{I}^{2}} \) (5.23)
Cần nói thêm rằng, năng lượng từ trường trong ống dây chỉ được tạo ra trong khoảng chừng thời hạn dòng điện trong mạch tăng từ không đến giá trị không thay đổi I. Vì kể từ sau thời gian đó, dòng điện trong mạch không còn biến thiên nữa, từ trường cũng đạt trạng thái không thay đổi và di = 0 nên ( 5.21 ) trở thành : \ ( dA = dQ \ ), nghĩa là năng lượng nguồn điện cung ứng chuyển hóa trọn vẹn thành nhiệt .Để chứng tỏ sự sống sót của năng lượng từ trường trong ống dây, ta chuyển khóa K từ tiếp điểm ( 1 ) sang tiếp điểm ( 2 ) thì thấy đèn lóe sáng một lúc rồi tắt. Khi khóa K chuyển sang tiếp điểm ( 2 ) thì mạch điện đã cô lập với nguồn điện. Vậy năng lượng ở đâu phân phối làm đèn lóe sáng ? Chỉ hoàn toàn có thể lý giải được đó là do năng lượng từ trường trong ống dây đã chuyển hóa thành điện năng làm lóe sáng đèn .
2. Năng lượng và mật độ năng lượng từ trường
Cũng như điện trường, năng lượng từ trường định xứ ở vùng khoảng trống có từ trường .Để tìm biểu thức tính năng lượng của từ trường đều trong ống dây solenoid, ta biến hóa biểu thức ( 5.23 ) bằng cách thay độ tự cảm : \ ( L = \ frac { { { \ mu } _ { 0 } } \ mu { { N } ^ { 2 } } S } { \ ell } = \ frac { { { \ mu } _ { 0 } } \ mu { { N } ^ { 2 } } } { { { \ ell } ^ { 2 } } } \ ell S = { { \ mu } _ { 0 } } \ mu { { n } ^ { 2 } } V \ ) ( 5.24 )Trong đó, n là tỷ lệ vòng dây và \ ( V = \ ell S \ ) là thể tích của ống dây, cũng là thể tích khoảng trống có từ trường .Thay ( 5.24 ) vào ( 5.23 ), ta được : \ ( { { W } _ { m } } = \ frac { 1 } { 2 } { { \ mu } _ { 0 } } \ mu { { n } ^ { 2 } } { { I } ^ { 2 } } V \ )Mà cảm ứng từ trong lòng ống dây là : \ ( B = { { \ mu } _ { 0 } } \ mu nI \ )Suy ra : \ ( { { W } _ { m } } = \ frac { 1 } { 2 } \ frac { { { B } ^ { 2 } } } { { { \ mu } _ { 0 } } \ mu } V \ ) ( 5.25 )Biểu thức ( 5.25 ) chứng tỏ năng lượng từ trường tỉ lệ thuận với thể tích khoảng trống có từ trường .
Đặt: \( {{\omega }_{m}}=\frac{{{B}^{2}}}{2{{\mu }_{0}}\mu }=\frac{BH}{2} \) (5.26)
Gọi là tỷ lệ năng lượng từ trường thì biểu thức tính năng lượng từ trường trong ống dây điện là : \ ( { { W } _ { m } } = { { \ omega } _ { m } } V \ ) ( 5.27 )Trong trường hợp tổng quát, nếu từ trường không đều thì ta chia nhỏ thể tích khoảng trống V thành những yếu tố thể tích đơn vị chức năng. Năng lượng từ trường chứa trong yếu tố thể tích đó là \ ( d { { W } _ { m } } = { { \ omega } _ { m } } dV \ ). Từ đó suy ra, năng lượng từ trường chứa trong toàn thể tích V là : \ ( { { W } _ { m } } = \ int \ limits_ { V } { { { \ omega } _ { m } } dV } = \ frac { 1 } { 2 } \ int \ limits_ { V } { BHdV } \ ) ( 5.28 )
Source: https://taimienphi.club
Category: Chưa phân loại