Hiện nay, có rất nhiều các bạn học sinh không nắm được chắc các kiến thức về hoán vị, chỉnh hợp, tổ hợp. Chính vì vậy, trong bài viết dưới đây chúng tôi sẽ chia sẻ tới các bạn công thức tính tổ hợp, chỉnh hơp, hoán vị và các dạng bài tập để các bạn cùng tham khảo nhé
Công thức hoán vị
Cho tập hợp A, gồm n thành phần ( n ≥ 1 ). Một cách sắp thứ tự n thành phần của tập hợp A được gọi là một hoán vị của n thành phần đó .
Kí hiệu số hoán vị của n phần tử là Pn
Công thức hoán vị :
Pn = n! = n(n – 1)…2.1
Hoán vị lặp là gì?
Giả sử một tập hợp có k thành phần được đánh số từ 1 đến k. Một cách sắp xếp k thành phần đó sao cho thành phần thứ i ( 1 ≤ i ≤ k ) Open n ( i ) lần và n ( 1 ) + n ( 2 ) + … + n ( k ) = n được gọi là một hoán vị lặp của k thành phần. Số hoán vị lặp là :
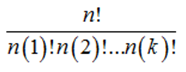
Công thức chỉnh hợp
Trong toán học, chỉnh hợp là cách chọn những thành phần từ một nhóm lớn hơn và có phân biệt thứ tự, trái với tổ hợp là không phân biệt thứ tự .
Theo định nghĩa, chỉnh hợp chập k của n thành phần là một tập con của tập hợp mẹ S chứa n thành phần, tập con gồm k thành phần riêng không liên quan gì đến nhau thuộc S và có sắp thứ tự. Số chỉnh hợp chập K của một tập S được tính theo công thức sau :
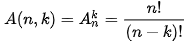
Chỉnh hợp không lặp
Cho tập A gồm n thành phần. Mỗi cách sắp xếp k thành phần của A ( 1 ≤ k ≤ n ) theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n thành phần của tập A .
Số chỉnh hợp chập k của n thành phần :
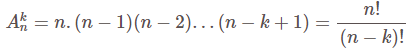
Khi k = n thì Ann = pn = n !
Chỉnh hợp lặp
Cho tập A gồm n thành phần. Mỗi dãy gồm k thành phần của A, trong đó mỗi thành phần hoàn toàn có thể được lặp lại nhiều lần, được sắp xếp theo một thứ tự nhất định được gọi là một chỉnh hợp chập k của n thành phần tập A .
Số chỉnh hợp lặp chập k của n thành phần : Akn = nk
Ngoài ra, những bạn hoàn toàn có thể tìm hiểu thêm thêm :
Công thức tổ hợp
Tổ hợp là cách chọn những thành phần từ một nhóm lớn hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn hoàn toàn có thể đếm được số tổ hợp .
Ví dụ cho ba loại quả, một quả táo, một quả cam và một quả lê, có ba cách tích hợp hai loại quả từ tập hợp này : một quả táo và một quả lê ; một quả táo và một quả cam ; một quả lê và một quả cam .
Công thức tổng hợp là :
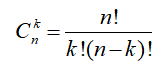
Tổ hợp không lặp
Cho tập A gồm n thành phần. Mỗi tập con gồm k ( 1 ≤ k ≤ n ) thành phần của A được gọi là một tổ hợp chập k của n thành phần của tập A .
Công thức tính tổ hợp chập k của n:

Tính chất:
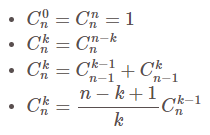
Tổ hợp lặp
Cho tập A = a1, a2, …, an và số tự nhiên k bất kể. Một tổ hợp lặp chập k của n thành phần là một tổ hợp gồm k thành phần, trong đó mỗi thành phần là một trong n thành phần của A .
Số tổ hợp lặp chập k của n thành phần :
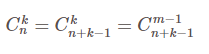
Phân biệt tổ hợp và chỉnh hợp
- Chỉnh hợp là bộ sắp có thứ tự: ví dụ, {a,b,c}, {a,c,b}, …
- Tổ hợp là bộ sắp không có thứ tự: ví dụ, {a,b,c} –> ok. Trong khi đó {a,c,b} và các cách sắp thứ tự kiểu khác của {a,b,c} không được tính là tổ hợp.
Bài tập về hoán vị, chỉnh hợp, tổ hợp
Ví dụ 1 : Sắp xếp 5 người vào một băng ghế có 5 chỗ. Hỏi có bao nhiêu cách .
Mỗi cách đổi chỗ 1 trong 5 người trên băng ghế là 1 hoán vị .
Vậy có P5 = 5 ! = 120 ( cách ) .
Ví dụ 2: Ông X có 11 người bạn. Ông ta muốn mời 5 người trong số họ đi chơi xa. Trong 11 người đó có 2 người không muốn gặp mặt nhau. Hỏi ông X có bao nhiêu cách mời?
Lời giải
Ông X chỉ mời 1 trong 2 người đó và mời thêm 4 trong số 9 người còn lại : 2. C49 = 252 .
Ông X không mời ai trong 2 người đó mà chỉ mời 5 trong số 9 người kia : C59 = 126
Suy ra 2. C49 + C59 = 2.126 + 126 = 252 + 126 = 378 cách
Ví dụ 3 : Cho tập hợp A = { 1,2,3,5,7,9 }
a. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau.
b. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn gồm có 5 chữ số đôi một khác nhau.
Lời giải :
a. Gọi số tự nhiên gồm 4 chữ số là :
![]()
Để có số n ta phải chọn đồng thời a1, a2, a3, a4 trong đó :
- a1 có 6 cách chọn
- a2 có 5 cách chọn
- a3 có 4 cách chọn
- a4 có 3 cách chọn
Vậy có 6.5.4. 3 = 360 số n cần tìm .
b. Gọi số tự chẵn có 5 chữ số cần tìm là
![]()
trong đó :
- a5 chỉ có 1 cách chọn (bằng 2)
- a1 có 5 cách chọn
- a2 có 4 cách chọn
- a3 có 3 cách chọn
- a4 có 2 cách chọn
Vậy số n cần tìm là : 1.2.3. 4.5 = 120 số .
Ví dụ 4 : Trên đường thẳng d1 cho 5 điểm phân biệt, trên đường thẳng d2 song song với đường thẳng d1 cho n điểm phân biệt. Biết có toàn bộ 175 tam giác được tạo thành mà 3 đỉnh lấy từ ( n + 5 ) điểm trên. Giá trị của n là
Lời giải
Để tạo thành một tam giác cần 3 điểm phân biệt
- Trường hợp 1: Chọn 1 điểm trên đường thẳng d1 và 2 điểm trên đường thẳng d2 có C15.C2n
- Trường hợp 2: Chọn 2 điểm trên đường thẳng d1 và 1 điểm trên đường thẳng d2 có C25.C1n
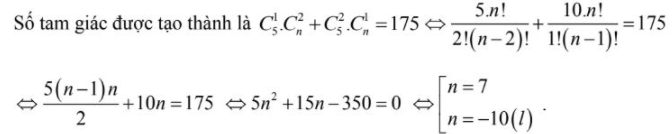
Sau khi đọc xong bài viết về công thức tổ hợp, chỉnh hợp, hoán vị mà chúng tôi đã trình diễn chi tiết cụ thể phía trên hoàn toàn có thể giúp những bạn vận dụng vào làm bài tập nhé
Đánh giá bài viết
Source: https://taimienphi.club
Category: Chưa phân loại
