Cách viết phương trình mặt cầu trong không gian Oxyz là chủ đề quan trọng trong chương trình toán học 12. Trong nội dung bài viết dưới đây, hãy cùng DINHNGHIA.VN tìm hiểu về cách viết phương trình mặt cầu trong không gian cũng như các dạng bài tập về viết phương trình mặt cầu, cùng tìm hiểu nhé!.
Định nghĩa mặt cầu là gì ? Lý thuyết phương trình mặt cầu
Khái niệm mặt cầu là gì ?
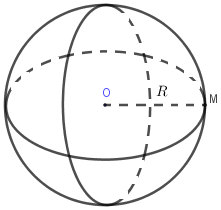
Mặt cầu được định nghĩa khi với điểm O cố định và thắt chặt cùng với 1 số ít thực dương R. Khi đó thì tập hợp tổng thể những điểm M trong khoảng trống cách O một khoảng chừng R sẽ được gọi là mặt cầu tâm O và bán kính R. Ký hiệu : S ( O ; R )
Các dạng phương trình mặt cầu

Cách viết phương trình mặt cầu trong không gian Oxyz
Trong khoảng trống với hệ tọa độ Oxyz, cho mặt cầu I ( a, b, c ) bán kính R. Khi đó phương trình mặt cầu tâm I ( a, b, c ) bán kính R có dạng là : \ ( ( x-a ) ^ { 2 } + ( b-y ) ^ { 2 } ) + ( c-z ) ^ { 2 } = R ^ { 2 } \ )
Hoặc : \ ( x ^ { 2 } + y ^ { 2 } + z ^ { 2 } – 2 ax – 2 cz + d = 0 \ ) với \ ( a ^ { 2 } + b ^ { 2 } + c ^ { 2 } > d \ )

Vị trí tương đối của mặt phẳng và mặt cầu
Cho mặt cầu ( S ) : \ ( ( x-a ) ^ { 2 } + ( b-y ) ^ { 2 } ) + ( c-z ) ^ { 2 } = R ^ { 2 } \ ) có tâm I, bán kính R và mặt phẳng ( P. ) : Ax + By + Cz + D = 0
Ta có khoảng cách d từ mặt cầu ( S ) đến mặt phẳng ( P. ) :
-
d > R: mặt phẳng (P) và mặt cầu (S) không có điểm chung.
-
d = R: mặt phẳng (P) và mặt cầu (S) tiếp xúc tại H.
-
d < R: mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có tâm K là hình chiếu của I trên (P) và bán kính \(r = \sqrt{R^{2} – d ^{2}}\).
Điểm H được gọi là tiếp điểm .
Mặt phẳng ( P. ) được gọi là tiếp diện .
Xem thêm >>>: Viết phương trình mặt phẳng trong không gian
Vị trí tương đối giữa đường thẳng và mặt cầu

Cho mặt cầu ( S ) : \ ( ( x-a ) ^ { 2 } + ( b-y ) ^ { 2 } ) + ( c-z ) ^ { 2 } = R ^ { 2 } \ ) có tâm I, bán kính R và đường thẳng \ ( \ Delta \ )
Ta có khoảng cách d từ mặt cầu ( S ) đến đường thẳng \ ( \ Delta \ ) :
- d > R : Đường thẳng \ ( \ Delta \ ) không cắt mặt cầu ( S )
- d = R : Đường thẳng \ ( \ Delta \ ) tiếp xúc với mặt cầu ( S )
- d < R : Đường thẳng \ ( \ Delta \ ) cắt mặt cầu ( S ) theo dây cung \ ( AB = \ sqrt { R ^ { 2 } – d ^ { 2 } } \ )
Xem thêm >>> Viết phương trình đường thẳng trong không gian Oxyz
Các dạng bài tập về viết phương trình mặt cầu
Dạng 1: Viết phương trình mặt cầu biết tâm và bán kính


Viết phương trình mặt cầu ( S ) có tâm \ ( I ( x_ { 0 }, y_ { 0 }, z_ { 0 } ) \ ) và bán kính R .
Thay tọa độ I và bán kính R vào phương trình, ta có :
( S ) : \ ( ( x – x_ { 0 } ) ^ { 2 } + ( y – y_ { 0 } ) ^ { 2 } + ( z – z_ { 0 } ) ^ { 2 } = R ^ { 2 } \ )
Ví dụ 2: Viết phương trình mặt cầu (S) có tâm I(3; -5; -2) và bán kính R = 5
Cách giải
Thay tọa độ của tâm I và bán kính R ta có phương trình mặt cầu ( S ) :
\ ( ( x – 3 ) ^ { 2 } + ( y – ( – 5 ) ) ^ { 2 } + ( z – ( – 2 ) ) ^ { 2 } = 5 ^ { 2 } \ Leftrightarrow ( x – 3 ) ^ { 2 } + ( y + 5 ) ^ { 2 } + ( z + 2 ) ^ { 2 } = 25 \ )

Dạng 2: Viết phương trình mặt cầu (S) có đường kính AB cho trước
- Tìm trung điểm của AB. Vì AB là đường kính nên I là tâm trung điểm AB đồng thời là tâm của mặt cầu .
- Tính độ dài IA = R .
- Làm tiếp như bài toán dạng 1 .
Ví dụ 2: Lập phương trình mặt cầu (S) có đường kính AB với A(4; −3; 7) và B(2; 1; 3)
Cách giải
Gọi I là trung điểm của AB, thì mặt cầu ( S ) có tâm I và bán kính .
\(r = \frac{AB}{2} = IA = IB\)
Ta có : Vì I là trung điểm của AB nên I có tọa độ \ ( I ( \ frac { 4 + 2 } { 2 } ; \ frac { – 3 + 1 } { 2 } ; \ frac { 7 + 3 } { 2 } ) \ Rightarrow I ( 3 ; – 1 ; 5 ) \ )
\ ( \ Rightarrow \ vec { IA } = ( 1 ; – 2 ; 2 ) \ )
\ ( \ Rightarrow R = \ left | \ vec { IA } \ right | = \ sqrt { 1 ^ { 2 } + ( – 2 ) ^ { 2 } + 2 ^ { 2 } } = 3 \ )
Thay tọa độ của tâm I và bán kính R ta có phương trình mặt cầu ( S ) :
\ ( ( x – 3 ) ^ { 2 } + ( y – ( – 1 ) ) ^ { 2 } + ( z – 5 ) ^ { 2 } = 3 ^ { 2 } \ Leftrightarrow ( x – 3 ) ^ { 2 } + ( y + 1 ) ^ { 2 } + ( z – 5 ) ^ { 2 } = 9 \ )
Dạng 3: Viết mặt cầu (S) qua 3 điểm A, B, C và có tâm thuộc mặt phẳng (P) cho trước.
- Gọi I ( a, b, c ) là tâm mặt cầu ( S ) thuộc mặt phẳng ( P. )
- Ta có hệ phương trình \ ( [ \ left \ { \ begin { matrix } IA = IB và \ \ IA = IC và \ \ I \ epsilon ( P. ) và \ end { matrix } \ right. \ )
- Giải hệ phương trình tìm được a, b, c sau đó thay vào 1 trong 2 phương trình trên để tìm bán kính mặt cầu .
Ví dụ 3: Viết phương trình mặt cầu (S) đi qua 3 điểm A (2;0;1), B (1;0;0), C (1;1;1) và có tâm thuộc mặt phẳng (P): x + y + z – 2 = 0.
Cách giải
Gọi phương trình tổng quát ( S ) : \ ( x ^ { 2 } + y ^ { 2 } + z ^ { 2 } + 2 ax + 2 by + 2 cz + d = 0 \ ) với \ ( a ^ { 2 } + b ^ { 2 } + c ^ { 2 } > d \ ) ( 1 )
Mặt cầu ( S ) có tâm \ ( I ( – a ; – b ; – c ) \ )
Từ đó ta có hệ phương trình :
\ ( \ left \ { \ begin { matrix } 4 + 1 + 4 a + 2 c + d = 0 và \ \ 1 + 2 c + d = 0 và \ \ 3 + 2 a + 2 b + 2 c + d = 0 và \ \ – a – b – c – 2 = 0 và \ end { matrix } \ right. \ )
\ ( \ Leftrightarrow \ left \ { \ begin { matrix } 4 a + 2 c + d = – 5 và \ \ 2 c + d = – 1 và \ \ 2 a + 2 b + 2 c + d = – 3 và \ \ a + b + b c = – 2 và \ end { matrix } \ right. \ )
\ ( \ Leftrightarrow \ left \ { \ begin { matrix } a = – 1 và \ \ b = 0 và \ \ c = – 1 và \ \ d = 1 và \ end { matrix } \ right. \ )
Vậy mặt cầu ( S ) có phương trình : \ ( x ^ { 2 } + y ^ { 2 } + z ^ { 2 } + 1 = 0 \ )
Trên đây là bài tổng hợp kiến thức về viết phương trình mặt cầu trong không gian cũng như các dạng bài tập viết phương trình mặt cầu. Cảm ơn các bạn đã đón đọc. Nếu có góp ý và thắc mắc hãy bình luận bên dưới để chúng mình giải đáp nhé <3
Xem chi tiết cụ thể qua bài giảng bên dưới :
(Nguồn: www.youtube.com)
Xem thêm :
4.7
/
5
(
4
bầu chọn
)
Please follow and like us :
![]()
![]()
Source: https://taimienphi.club
Category: Chưa phân loại
