Công thức nguyên hàm, bảng nguyên hàm đầy đủ & mở rộng

Tổng hợp công thức nguyên hàm, bảng nguyên hàm đầy đủ, chi tiết & mở rộng. Giúp các em học sinh nắm vững trước khi làm bài tập. Bài học thuộc chương 3 của chương trình toán lớp 12, một trong những chuyên đề quan trọng trong các kì thi và có nhiều ứng dụng trong thực tiễn.

Bài học liên quan

Bạn đang đọc: Công thức nguyên hàm, bảng nguyên hàm đầy đủ & mở rộng

Nguyên hàm và những đặc thù

1. Khái niệm nguyên hàm

Định nghĩa : Cho hàm số f ( x ) xác lập trên K ( K là khoảng chừng hoặc đoạn hoặc nửa đoạn của ℝ ). Hàm số F ( x ) được gọi là nguyên hàm của hàm số f ( x ) trên K nếu F ’ ( x ) = f ( x ) với mọi x ∊ K .

Định lý 1: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
Định lý 2: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) đều có dạng F(x) + C, với C là một hằng số.

Hai định lý trên cho thấy :Nếu F ( x ) là một nguyên hàm của hàm số f ( x ) trên K thì F ( x ) + C, C ∊ ℝ là họ tổng thể những nguyên hàm của f ( x ) trên K. Kí hiệu :

Chú ý : Biểu thức f ( x ) dx chính là vi phân của nguyên hàm F ( x ) của f ( x ), vì dF ( x ) = F ’ ( x ) ․ dx = f ( x ) ․ dx .

2. Tính chất của nguyên hàm

Tính chất 1

Tính chất 2

, k là hằng số khác 0.

Tính chất 3

, k là hằng số khác 0 .

3. Sự tồn tại của nguyên hàm

Định lý 3 : Mọi hàm số f ( x ) liên tục trên K đều có nguyên hàm trên K .

Bảng công thức nguyên hàm vừa đủ

Thông thường, trong quy trình khởi đầu tiếp xúc nguyên hàm thì việc ghi nhớ những công thức là điều rất khó khăn vất vả và mất nhiều thời hạn. Bảng nguyên hàm dưới dạng file PDF mà VerbaLearn tổng hợp sẽ giúp những bạn học viên tra cứu trong quy trình học tập. Quen dần, những công thức sử dụng nhiều sẽ giúp những em nhớ kĩ và ứng dụng một cách thuần thục hơn .

1. Nguyên hàm của hàm số sơ cấp

2. Nguyên hàm của hàm số hợp (u = u(x))

Nguyên hàm của hàm số hợp (u = ax + b; a ≠ 0)

$\int {\frac{1}{{{{\cos }^2}(ax + b)}}dx = \frac{1}{a}} \tan (ax + b) + C$
$\int {\frac{1}{{\sin (ax + b)}}dx = \frac{1}{a}} \ln \left| {\tan \frac{{ax + b}}{2}} \right| + C$
$\int {\frac{1}{{\cos (ax + b)}}dx = \frac{1}{a}} \ln \left| {\tan \frac{{ax + b}}{2} + \frac{\pi }{4}} \right| + C$

Phương pháp tính nguyên hàm

1. Phương pháp cơ bản

Định lý 1: Nếu

và u = u(x) có đạo hàm liên tục thì:và u = u ( x ) có đạo hàm liên tục thì :

Hệ quả : Với u = ax + b ( a ≠ 0 ) ta có

2. Phương pháp tính nguyên hàm từng phần

Định lý 2 : Nếu hai hàm số u = u ( x ) và v = v ( x ) có đạo hàm liên tục trên K thì

Ở phần phân loại bài tập, tất cả chúng ta sẽ tìm hiểu và khám phá kĩ càng hơn chiêu thức này .

Phân loại và giải pháp giải bài tập nguyên hàm

Dạng 1: Tìm nguyên hàm bằng các biến đổi sơ cấp

Phương pháp giải

Biến đổi những hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của những biểu thức chứa x, trong đó mỗi biểu thức chứa x là những dạng cơ bản có trong bảng nguyên hàm .Áp dụng những công thức nguyên hàm trong bảng nguyên hàm cơ bản để tìm nguyên hàm .

Bài tập vận dụng

Bài tập 1: Nguyên hàm của hàm số là

Hướng dẫn giải

Chọn C.

Ta có

Bài tập 2: Nguyên hàm của hàm số f (x) = x (x + 2)2019 là

Hướng dẫn giải

Chọn D.

Ta có:

Bài tập 3: Nguyên hàm của hàm số là

C. ln ( e2x + 1 ) + CD. x – ln ( e2x + 1 ) + C

Hướng dẫn giải

Chọn B.

Ta có:

Do đó

Bài tập 4: Nguyên hàm của hàm số là

Hướng dẫn giải

Chọn A.

Ta có:

Chú ý: Sử dụng kĩ thuật nhân liên hợp:

Lưu ý:

Bài tập 5: Nguyên hàm của hàm số là

A. 2 ln | x – 3 | – 3 ln | x + 2 | + CB. 3 ln | x – 3 | + 2 ln | x – 2 | + CC. 2 ln | x + 3 | + 3 ln | x + 2 | + CD. 2 ln | x – 3 | + 3 ln | x – 2 | + C

Hướng dẫn giải

Chọn D.

Ta có:

Ta sẽ nghiên cứu và phân tích : 5 x – 13 = A ( x – 2 ) + B ( x – 3 ) ( 1 )Thế x = 2 và x = 3 lần lượt vào ( 1 ) ta có B = 3 và A = 2 .

Khi đó

= 2 ln | x – 3 | + 3 ln | x – 2 | + C

Bài tập 6: Nguyên hàm của hàm số là

Hướng dẫn giải

Chọn C.

Ta có

Bài tập 7: Nguyên hàm của hàm số là:

Hướng dẫn giải

Chọn A.

Ta có:

Ta nghiên cứu và phân tích 3×2 + 3 x + 3 = A ( x – 1 ) 2 + B ( x – 1 ) ( x + 2 ) + C ( x + 2 ) .Ta hoàn toàn có thể dùng những giá trị riêng, tính ngay A = 1, C = 3 và B = 2 .( Thay x = – 2 ⇒ A = 1 ; x = 1 ⇒ C = 3 và x = 0 ⇒ B = 2 ) .

Khi đó:

Lưu ý: Ta có kiến thức tổng quát dùng cho các nguyên hàm hữu tỉ

, với P(x) và Q(x) là các đa thức, cụ thể như sau:, với P. ( x ) và Q. ( x ) là những đa thức, đơn cử như sau :Nếu deg ( P. ( x ) ) ≥ deg ( Q. ( x ) ) thì ta triển khai phép chỉa P. ( x ) cho Q. ( x ) ( ở đây, kí hiệu deg ( P. ( x ) ) là bậc của đa thức P. ( x ) ) .Khi deg ( P. ( x ) ) < deg ( Q. ( x ) ) thì ta quan sát mẫu số Q. ( x ) ta triển khai nghiên cứu và phân tích thành những nhân tử, sau đó, tách P. ( x ) theo những tổng hợp của những nhân tử đó. Đến đây, ta sẽ sử dụng đồng nhất thức ( hoặc giá trị riêng ) để đưa về dạng tổng của phân thức .Một số trường hợp đồng nhất thức thường gặp

Trường hợp 1:

Trường hợp 2:

Ta đồng nhất thức mx + n = ( Ax + Ba ) x + Ad + Bb ( 1 ) .

Cách 1: Phương pháp đồng nhất hệ số.

Đồng nhất đẳng thức, ta được

. Suy ra A, B.

Cách 2: Phương pháp giá trị riêng.

. Suy ra A, B .

Lần lượt thay

vào hai vế của (1), tìm được A, B.vào hai vế của ( 1 ), tìm được A, B .

Trường hợp 3:

Trường hợp 4:

Lần lượt thay; x = 0 vào hai vế của (*) để tìm A, B, C.; x = 0 vào hai vế của ( * ) để tìm A, B, C .

Trường hợp 5:

với ∆ = b2 – 4ac < 0.với ∆ = b – 4 ac < 0 .

Trường hợp 6:

Bài tập 8: Cho hàm số f(x) xác định trên ℝ\ thỏa mãn ; f (0) = 1 và f (1) = 2. Giá trị của biểu thức P = f (–1) + f (3) là:

A. 3 ln5 + ln2B. 3 ln2 + ln5C. 3 + 2 ln5D. 3 + ln15

Hướng dẫn giải

Chọn D.

Vì

Suy ra

Do đó P = f ( – 1 ) + f ( 3 ) = 3 + ln 3 + ln 5 = 3 + ln15 .

Bài tập 9: Cho hàm số f (x) xác định trên ℝ \ {–1; 1}, thỏa mãn ; f (–3) + f (3) = 2 ln2 và . Giá trị của biểu thức P = f (–2) + f (0) + f (4) là:

A. 2 ln2 – ln5B. 6 ln2 + 2 ln3 – ln5C. 2 ln2 + 2 ln3 – ln5D. 6 ln2 – 2 ln5

Hướng dẫn giải

Chọn C.

Hay

Theo bài ra, ta có:

Do đó

Bài tập 10: Nguyên hàm là:

Hướng dẫn giải

Chọn A.

Ta có:

Bài tập 11: Nguyên hàm của hàm số là

Hướng dẫn giải

Chọn B.

Ta có:

Bài tập 12: Nguyên hàm của hàm số là:

A. – tan x – cot x + CB. tan x – cot x + CC. tan x + cot x + CD. cot x – tan + C

Hướng dẫn giải

Chọn B.

Ta có:

Bài tập 13: Nguyên hàm của hàm số là:

B. tan 2 x + CC. cot 2 x + C

Hướng dẫn giải

Chọn D.

Ta có:

Bài tập 14: Nguyên hàm của hàm số là

Hướng dẫn giải

Chọn A.

Từ tan3 x = tan x ( 1 + tan2 x ) – tan x

Suy ra

Bài tập 15: Gọi F(x) là nguyên hàm của hàm số f(x) = sin2x tanx thỏa mãn . Giá trị của là:

Hướng dẫn giải

Chọn D.

Ta có:

Suy ra

Theo giả thiết, ta có:

Vậy

Do đó

Bài tập 16: Gọi F(x) là nguyên hàm của hàm số f(x) = cos4 2x thỏa mãn F (0) = 2019. Giá trị của là

Hướng dẫn giải

Chọn C.

Ta có:

Do đó

Mà F ( 0 ) = 2019 nên ta có C = 2019 .

Vậy

Do đó =

Bài tập 17: Gọi F(x) là nguyên hàm của hàm số , với , k ∊ ℤ và thỏa mãn . Giá trị của là:

B. 0

Hướng dẫn giải

Chọn D.

Ta thấy:

Theo giả thiết, ta có nên C = 1.nên C = 1 .

Vậy

Do đó = Chú ý : Với n ∊ ℕ *, ta có :

và

Bài tập 18: Biết là phân số tối giản. Giá trị 2a – b là

vàA. 10B. – 4C. 7D. – 3

Hướng dẫn giải

Chọn D.

Vậy a = 1, b = 5. Nên 2 a – b = – 3 .

Bài tập 19: Tìm một nguyên hàm của F(x) của hàm số f(x) = (1 + sinx)2 biết .

Hướng dẫn giải

Chọn B.

Ta có:

Vậy

Bài tập 20: Cho và F (π) = a + b. Tính A = (a + b)6.

A. – 2B. 2C. 1D. – 1

Hướng dẫn giải

Chọn C.

Ta có

⇒ F ( π ) = – 1 = a + b ⇒ A = 1

Bài tập 21: Cho tích phân . Tính A = 12 cot2 2x theo a.

A. 4 a2B. 2 a2C. 3 a2D. a2

Hướng dẫn giải

Chọn C.

Ta có:

= tan x – cot x .

Theo đề:

Bài tập 22: Cho F(x) là một nguyên hàm của hàm số và . Tính .

C. 0D. 1

Hướng dẫn giải

Chọn B.

Ta cód ( cos2 x + 4 sin2 x ) = ( – 2 sinx cosx + 8 sinx cosx ) dx = 6 sinx cosx dx = 3 sin2x dx

.Do đó =

Vậy

Bài 23: Gọi F(x) là nguyên hàm của hàm số trên khoảng thỏa mãn F (2) = 0. Khi đó phương trình F(x) = x có nghiệm là:

A. x = 0B. x = 1C. x = – 1

Hướng dẫn giải

Chọn D.

Ta có:

Mặt khác:

Vậy

Xét phương trình F(x) = x

Bài tập 24: Cho F(x) là một nguyên hàm của hàm số trên khoảng (0; +∞) và . Tổng S = F (1) + F (2) + F (3) + … + F (2019) là

Hướng dẫn giải

Chọn C.

Phân tích

Khi đó

Mặt khác

Vậy

Do đó S = F (1) + F (2) + F (3) + … + F (2019) =

Bài tập 25: Cho hàm số f(x) có đạo hàm liên tục xác định trên ℝ thỏa mãn , f(x) > 0 và , ∀ x ∊ ℝ. Giá trị f (1) là:

Hướng dẫn giải

Chọn D.

Ta có:

Suy ra

Theo giả thiết, suy ra , suy ra

Với C = 3 thì

Vậy

Bài tập 26: Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [–2; 1] thỏa mãn f (0) = 3 và (f(x))2. f’(x) = 3×2 + 4x + 2. Giá trị lớn nhất của hàm số y = f(x) trên đoạn [–2; 1] là:

Hướng dẫn giải

Chọn C.

Ta có : ( f ( x ) ) 2. f ’ ( x ) = 3×2 + 4 x + 2 ( * )Lấy nguyên hàm hai vế của đẳng thức ( * ) ta được :

⇔ f 3(x) = 3×3 + 6×2 + 6x + 3C⇔ f ( x ) = 3 x + 6 x + 6 x + 3CTheo giả thiết, ta có f ( 0 ) = 3 nên( f ( 0 ) ) 3 = 3 ( 03 + 2. 02 + 2. 0 + C ) ⇔ 27 = 3C ⇔ C = 9 ⇒ f 3 ( x ) = 3×3 + 6×2 + 6 x + 27Ta tìm giá trị lớn nhất của hàm số g ( x ) = 3×3 + 6×2 + 2 x + 27 trên đoạn [ – 2 ; 1 ] .Ta có g ’ ( x ) – 9×2 + 12 x + 6 > 0, ∀ x ∊ [ – 2 ; 1 ] nên đồng biến trên đoạn [ – 2 ; 1 ] .

Vậy

Dạng 2: Phương pháp đổi biến dạng 1, đặt u = u(x)

Phương pháp giải

Định lí: Cho

và u = u(x) là hàm số có đạo hàm liên tục thìvà u = u ( x ) là hàm số có đạo hàm liên tục thì

Các bước triển khai đổi biến :

Xét

Bước 1

Đặt u = u ( x ), suy ra du = u ’ ( x ) dx

Bước 2

Chuyển nguyên hàm ban đầu về ẩn u ta được

, trong đó F(u) là một nguyên hàm của hàm số f(u).

Bước 3

, trong đó F ( u ) là một nguyên hàm của hàm số f ( u ) .Trả về biến x khởi đầu, ta có nguyên hàm cần tìm là I = F ( u ( x ) ) + C

Hệ quả: nếu F(x) là một nguyên hàm của hàm số f(x) trên K và a, b ∊ ℝ; a ≠ 0 ta có:

Bài tập vận dụng

Bài tập 1: Nguyên hàm F(x) của hàm số , biết là:

Hướng dãn giải

Chọn D.

Đặt u = x3 + 1 ta có

Suy ra

Do đó

Mặt khác nên C = 0. Vậy nên C = 0. Vậy

Lưu ý: Ta có thể viết như sau:

Chú ý: Với các viết

, ta có tính nguyên hàm đã cho một cách đơn giản và nhanh gọn.

Bài tập 2: Nguyên hàm là

, ta có tính nguyên hàm đã cho một cách đơn thuần và nhanh gọn .

Hướng dẫn giải

Chọn C.

Đặt u = 1 + 3 cosx, ta có du = –3 sinx dx hay

Khi đó

Vậy =

Bài tập 3: , (a, b ∊ ℤ+). Tìm tỉ lệ .

Hướng dẫn giải

Chọn B.

Đặt

Và

thì thì

Bài tập 4: Cho và .

Tính A = a2 + b2 + 2018 .A. 2018B. năm nayC. 2022D. 2020

Hướng dẫn giải

Chọn A.

Đặt u = cos x ⇒ – du = sinx dx .

A = a3 + b3 + 2018 = ( a + b ) 2 – 2 ab ( a + b ) + 2018 = 2018 .

Chú ý: chú ý rằng với a > 0 và m, n ∊ ℤ; n > 0 ta luôn có:

Bài tập 5: Nguyên hàm là:

Hướng dẫn giải

Chọn D.

Đặt

. Suy ra x = u2 – 1 và dx = 2udu.. Suy ra x = u – 1 và dx = 2 udu .

Khi đó

Vậy

Bài tập 6: Nguyên hàm là:

Xem thêm: Top 16 điệu cười của nicolas cage mới nhất 2022

Hướng dẫn giải

Chọn A.

Xét

Đặt

. Suy ra x2 = u2 – 9 và xdx = udu.. Suy ra x = u – 9 và xdx = udu .

Khi đó

Vậy

Bài tập 7: Nguyên hàm là:

Hướng dẫn giải

Chọn B.

Ta có:

Bài tập 8: Nguyên hàm là

Hướng dẫn giải

Chọn C.

Xét

Đặt

Suy raLưu ý :

Bài tập 9: Xét nguyên hàm . Đặt , khẳng định nào sau đây sai?

Hướng dẫn giải

Chọn C.

Đặt

Khi đó

Bài tập 10: Gọi F(x) là nguyên hàm của hàm số f(x) = sin2 2x. cos3 2x thỏa . Giá trị F (2019π) là:

Hướng dẫn giải

Chọn A.

Đặt

Ta có

Vậy

Do đó

Bài tập 11: Biết rằng (với C là hằng số). Gọi S là tập nghiệm của phương trình g(x) = 0. Tổng các phần tử của S bằng:

A. 0

C. – 3

Hướng dẫn giải

Chọn C.

Vì x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 = ( x2 + 3 x ) ( x2 + 3 x + 2 ) + 1 = [ ( x2 + 3 x ) + 1 ] 2 nên ta đặt u = x2 + 3 x, khi đó du = ( 2 x + 3 ) dx

Nguyên hàm ban đầu trở thành

Suy ra

Vậy

Do đó

Tổng giá trị những thành phần của S bằng – 3 .

Bài tập 12: . Tính F (1), biết rằng F(x) không chứa hệ số tự do.

Hướng dẫn giải

Chọn A.

Đặt

Dạng 3: Tìm nguyên hàm bằng cách đổi biến dạng 2

Phương pháp giải

Ta đã biết những đẳng thức sau :sin2 t + cos2 t = 1, với mọi t ∊ ℝ .

(k ∊ ℤ)( k ∊ ℤ )

(k ∊ ℤ)( k ∊ ℤ )Với những bài toán sau đây thì ta không hề xử lý ngay bằng nguyên hàm cơ bản cũng như đổi biến số ở dạng 1, yên cầu người học phải trang bị tư duy đổi biến theo kiểu “ lượng giác hóa ” dựa vào những hằng đẳng thức lượng giác cơ bản và một số ít biến hóa thích hợp, đơn cử ta xem những nguyên hàm sau đây :

Bài toán 1: Tính
Bài toán 2: Tính
Bài toán 3: Tính
Bài toán 4: Tính
Bài toán 5: Tính

Các kỹ thuật đổi biến dạng 2 thường gặp và cách xử líBài toán 1 : Tính

Đặt x = |a| sint, với

hoặc x = |a| cost với t ∊ (0; π)hoặc x = | a | cost với t ∊ ( 0 ; π )Bài toán 2 : TínhĐặt x = | a | tant, vớiBài toán 3 : Tính

Đặt x = a cos2t với

Bài toán 4 : Tính

Đặt x = a + (b – a) sin2 t với

Bài toán 5 : Tính

Đặt

với

Bài tập vận dụng

Bài tập 1: Nguyên hàm là:

với

Hướng dẫn giải

Chọn D.

Đặt x = 2 sint với. Ta có cost > 0 và dx = 2 costdt.. Ta có cost > 0 và dx = 2 costdt .

Khi đó

vì cost > 0, ∀ vì cost > 0, ∀

Suy ra

Từ

và vàVậy =

Bài tập 2: Nguyên hàm là:

Hướng dẫn giải

Chọn B.

Đặt x = cost, t < 0 < π ⇒ dx = – sint dt

Khi đó

Vậy =

Bài tập 3: Nguyên hàm là:

A. arctan x + CB. arccot x + CC. arcsin x + CD. arccos x + C

Hướng dẫn giải

Chọn A.

Đặt x = tant với, ta có dx = (1 + tan2 t) dt., ta có dx = ( 1 + tant ) dt .

Khi đó

Vậy = arctan x + C

Dạng 4: Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần

Phương pháp giải

= arctan x + CVới u = u ( x ) và v = v ( x ) là những hàm số có đạo hàm trên khoảng chừng K thì ta có : ( u. v ) ’ = u’v. v’uViết dưới dạng vi phân d ( uv ) = vdu + udv

Khi đó lấy nguyên hàm hai vế ta được:

Từ đó suy ra

(1)( 1 )Công thức ( 1 ) là công thức nguyên hàm từng phần .Dấu hiệu nhận ra phải sử dụng giải pháp nguyên hàm từng phần .

Bài toán: Tìm

, trong đó u(x) và v(x) là hai hàm số có tính chất khác nhau, chẳng hạn:, trong đó u ( x ) và v ( x ) là hai hàm số có đặc thù khác nhau, ví dụ điển hình :u ( x ) là hàm số đa thức, v ( x ) là hàm số lượng giác .u ( x ) là hàm số đa thức, v ( x ) là hàm số mũ .u ( x ) là hàm số logarit, v ( x ) là hàm số đa thức .u ( x ) là hàm số mũ, v ( x ) là hàm số lượng giác .Phương pháp nguyên hàm từng phần

Bước 1: Đặt

Bước 2 : Áp dụng công thức ( 1 ), ta được :Lưu ý : Đặt u ( x ) ( ưu tiên ) theo thứ tự : “ Nhất lốc, nhì đa, tam lượng, tứ mũ ”. Tức là, nếu có logarit thì ưu tiên đặt u là logarit, không có logarit thì ưu tiên u là đa thức, … thứ tự ưu tiên sắp xếp như vậy .

Còn đối với nguyên hàm

ta chỉ cần Chọn một hằng số thích hợp. Điều này sẽ được làm rõ qua các Bài tập minh họa ở cột bên phải.

Bài tập vận dụng

Bài tập 1: Kết quả nguyên hàm là:

ta chỉ cần Chọn một hằng số thích hợp. Điều này sẽ được làm rõ qua những Bài tập minh họa ở cột bên phải .

Hướng dẫn giảiChọn D .

Đặt

Khi đó

Chú ý: Thông thường thì với

Tuy nhiên trong trường hợp này, ta để ý

mang lại sự hiệu quả.

Bài tập 2: Kết quả nguyên hàm là:

Hướng dẫn giải

Chọn B.

Đặt

Khi đó

= ( tanx + 2 ). ln ( sinx + 2 cosx ) – x – 2 ln | cosx | + C

Chú ý: Ở bài tập này, Chọn v = tanx + 2 có thể rút gọn được ngay tử và mẫu trong nguyên hàm

Bài tập 3: Kết quả nguyên hàm là:

Hướng dẫn giải

Chọn D.

Phân tích : Ở đây ta sẽ ưu tiên u = x2 là đa thức, tuy nhiên vì bậc của u là 2 nên ta sẽ từng phần hai lần mới thu được tác dụng. Nhằm tiết kiệm chi phí thời hạn, tôi gợi ý với chiêu thức “ sơ đồ đường chéo ” đơn cử như sau :Bước 1 : Chia thành 3 cột :Cột 1 : Cột u luôn lấy đạo hàm đến 0 .Cột 2 : Dùng để ghi rõ dấu của những phép toán đường chéo .Cột 3 : Cột dv luôn lấy nguyên hàm đến khi tương ứng với cột 1 .Bước 2 : Nhân chéo hiệu quả của hai cột với nhau. Dấu của phép nhân tiên phong sẽ có dấu ( + ), sau đó đan dấu ( – ), ( + ), ( – ), … rồi cộng những tích lại với nhau .

Khi đó:

Chú ý :Kĩ thuật này rất đơn thuần và tiết kiệm ngân sách và chi phí nhiều thời hạn .Trong kĩ thuật tìm nguyên hàm theo sơ đồ đường chéo, nhu yếu fan hâm mộ cần thống kê giám sát đúng chuẩn đạo hàm và nguyên hàm ở hai cột 1 và 3. Nếu nhầm lẫn thì rất đáng tiếc .

Bài tập 4: Nguyên hàm là:

Hướng dẫn giải

Chọn A.

Nếu làm thường thì thì từng phần 4 lần ta mới thu được tác dụng. Ở đây, chúng tôi trình diễn theo sơ đồ đường chéo cho hiệu quả và nhanh gọn hơn .

Vậy

Bài tập 5: Nguyên hàm là:

A. 2 ex ( sinx + cosx ) + CB. 2 ex ( sinx – cosx ) + C

Hướng dẫn giải

Chọn C.

Phân tích : Sự sống sót của hàm số mũ và lượng giác trong cùng một nguyên hàm sẽ rất dễ gây cho người học sự nhầm lẫn, nếu ta sẽ không biết điểm dừng thì hoàn toàn có thể sẽ bị lạc vào vòng luẩn quẩn. Ở đây, để tìm được hiệu quả thì ta phải từng phần hai lần như trong bài tập 3. Tuy nhiên, với sơ đồ đường chéo thì sao ? Khi nào sẽ dừng lại ?

Khi đó, ta sẽ có thể kết luận

Hay 2I = ex sinx – ex. cos x. Vậy

Chú ý: Chỉ dừng lại khi đạo hàm của nó có dạng giống dòng đầu tiên. Dòng cuối thu được

Bài tập 6: Tìm , trong đó v(x) là hàm đa thức, n ∊ ℕ* và a, b ∊ ℝ; a ≠ 0

Hướng dẫn giải

Phân tích: Vì ưu tiên u(x) = lnn (ax + b) nên

và tiếp tục đạo hàm thì cột 1 sẽ không về 0 được, vì vậy phải chuyển lượng từ cột 1 sang nhân với v(x) ở cột 3 để rút gọn bớt; tiếp tục quá trình như thế nào cho đến khi đạo hàm cột 1 về 0, và chú ý sử dụng quy tắc đan dấu bình thường.

Bài tập 6.1: Kết quả nguyên hàm là:

và liên tục đạo hàm thì cột 1 sẽ không về 0 được, vì thế phải chuyển lượngtừ cột 1 sang nhân với v ( x ) ở cột 3 để rút gọn bớt ; liên tục quy trình như thế nào cho đến khi đạo hàm cột 1 về 0, và quan tâm sử dụng quy tắc đan dấu thông thường .

Hướng dẫn giải

Chọn A.

Vậy =

Chú ý: chuyển lượng

bên cột 1 sang nhân với ta thu được kết quả . Khi đó bên cột 1 còn lại 1, đạo hàm của nó bằng 0; bên cột 3 có nguyên hàm của là .

Bài tập 6.2: Kết quả nguyên hàm là:

bên cột 1 sang nhân vớita thu được hiệu quả. Khi đó bên cột 1 còn lại 1, đạo hàm của nó bằng 0 ; bên cột 3 có nguyên hàm củalà

Hướng dẫn giải

Chọn B.

VậyChú ý :

Chuyển

, nhân với (2×2 – x) thu được (6x – 3)., nhân với ( 2 x – x ) thu được ( 6 x – 3 ) .

Chuyển

, nhân với (3×2 – 3x) thu được (6x – 6)., nhân với ( 3 x – 3 x ) thu được ( 6 x – 6 ) .

Chuyển

, nhân với (3×2 – 6x) thu được (3x – 6).

Bài tập 7: Cho F(x) = (x – 1) ex là một nguyên hàm f(x) e2x. Biết rằng hàm số f(x) có đạo hàm liên tục trên ℝ. Nguyên hàm của hàm số f’(x) e2x là:

, nhân với ( 3 x – 6 x ) thu được ( 3 x – 6 ) .A. ( 2 – x ) ex + CB. ( 2 + x ) ex + CC. ( 1 – x ) ex + CD. ( 1 + x ) ex + C

Hướng dẫn giải

Chọn A.

Ta có F ’ ( x ) = f ( x ) e2x ⇔ ex + ( x – 1 ) ex = f ( x ). e2x ⇔ f ( x ). e2x = x. ex .

Xét

Đặt

Do đó

Vậy

Dạng 5: Các bài toán thực tế ứng dụng nguyên hàm

Phương pháp giải

Ý nghĩa vật lí của đạo hàm :Một chất điểm hoạt động theo phương trình S = S ( t ), với S ( t ) là quãng đường mà chất điểm đó đi được trong thời hạn t, kể từ thời gian bắt đầu .Gọi v ( t ) và a ( t ) lần lượt là tốc độ tức thời và tần suất tức thời của chất điểm tại thời gian t, ta có :v ( t ) = S ’ ( t ) và a ( t ) = v ’ ( t ) .

Từ đó ta có:

và

Bài tập vận dụng

Bài tập 1: Một vật chuyển động với gia tốc , trong đó t là khoảng thời gian tính từ thời điểm ban đầu. Vận tốc ban đầu của vật là. Hỏi vận tốc của vật tại giây thứ 10 bằng bao nhiêu?

vàA. 10 m / sB. 15,2 m / sC. 13,2 m / sD. 12 m / s

Hướng dẫn giải

Chọn C.

Vận tốc của vật tại thời điểm t được tính theo công thức:

Vì tốc độ khởi đầu ( lúc t = 0 ) của vật là v0 = 6 m / s nên :v ( 0 ) = 3 ln | 0 + 1 | + C = 6 ⇔ C = 6 ⇒ v ( t ) = 3 ln | t + 1 | + 6 .Vận tốc của vật hoạt động tại giây thứ 10 là : v ( 10 ) = 3 ln | 10 + 1 | + 6 ≈ 13,2 ( m / s ) .

Bài tập 2: Một vận động viên điền kinh chạy với gia tốc , trong đó t là khoảng thời gian tính từ lúc xuất phát. Hỏi vào thời điểm 5 (s) sau khi xuất phát thì vận tốc của vận động viên là bao nhiêu?

A. 5,6 m / sB. 6,51 m / sC. 7,26 m / sD. 6,8 m / s

Hướng dẫn giải

Chọn B.

Vận tốc v ( t ) chính là nguyên hàm của tần suất a ( t ) nên ta có :

Tại thời gian khởi đầu ( t = 0 ) thì vận động viên ở tại vị trí xuất phát nên tốc độ lúc đó là :

Vậy công thức vận tốc là

Vận tốc của vận động viên tại giây thứ 5 là v ( 5 ) = 6,51 m / s .

Chú ý: Gia tốc của vật chuyển động là

. Ta tính , kết hợp với điều kiện vận tốc ban đầu v0 = 6 m/s. Suy ra công thức tính vận tốc v(t) tại thời điểm t và tính được v(10).

Bài tập 3: Một nhà khoa học tự chế tên lửa và phóng tên lửa từ mặt đát với vận tốc ban đầu là 20 m/s. Giả sử bỏ qua sức cản của gió, tên lửa chỉ chịu tác động của trọng lực. Hỏi sau 2s thì tên lửa đạt đến tốc độ là bao nhiêu?

. Ta tính, tích hợp với điều kiện kèm theo tốc độ khởi đầu v = 6 m / s. Suy ra công thức tính tốc độ v ( t ) tại thời gian t và tính được v ( 10 ) .A. 0,45 m / sB. 0,4 m / sC. 0,6 m / sD. 0,8 m / s

Hướng dẫn giải

Chọn B.

Xem như tại thời gian t0 = 0 thì nhà khoa học phóng tên lửa với tốc độ đầu 20 m / s. Ta có s ( 0 ) = 0 và v ( 0 ) = 20 .Vì tên lửa hoạt động thẳng đứng nên tần suất trọng trường tại mọi thời gian t là sn ( t ) = – 9,8 m / s2 .

Nguyên hàm của gia tốc là vận tốc nên ta có vận tốc của tên lửa tại thời điểm t là

Do v ( 0 ) = 20 nên – 9,8 t + C1 = 20 ⇔ C1 = 20 ⇒ v ( t ) = – 9,8 t + 20 .Vậy tốc độ của tên lửa sau 2 s là v ( 2 ) = – 9,8. 2 + 20 = 0,4 ( m / s ) .

Tài liệu hay nhất về nguyên hàm

Dưới đây là một số ít tài liệu hay nhất cho chuyên đề nguyên hàm, công thức nguyên hàm và những dạng toán ứng dụng. Bạn hoàn toàn có thể lựa chọn tài liệu tương thích trải qua phần miêu tả sau đó tải về để tiện cho việc tra cứu hoặc làm bài tập. Các tài liệu đều được đóng bằng file PDF .

#1. Nguyên hàm, tích phân và ứng dụng

Thông tin tài liệu
Tác giả	GeoGebraPro
Số trang	827
Lời giải chi tiết	Có

Mục lục tài liệu

Nguyên hàm và tính chất
Phương pháp tính nguyên hàm
Phương pháp tính nguyên hàm đổi biến số
Phương pháp tính nguyên hàm từng phần
Bảng nguyên hàm cơ bản
Bảng nguyên hàm mở rộng
Tính nguyên hàm bằng bảng nguyên hàm
Tìm nguyên hàm bằng phương pháp đổi biến số
Nguyên hàm từng phần

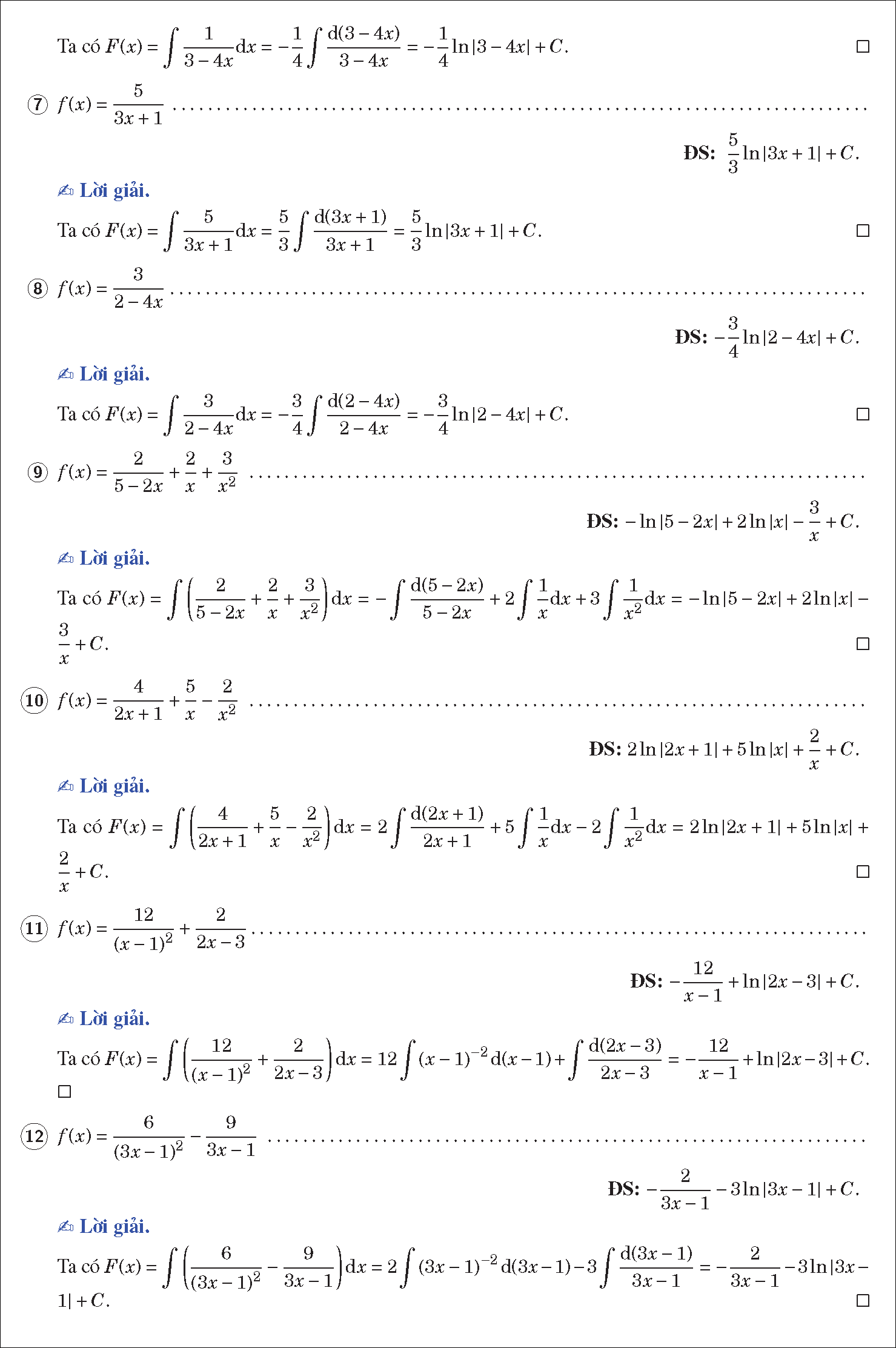
#2. Các dạng bài tập VDC nguyên hàm và một số phương pháp tìm nguyên hàm

Thông tin tài liệu
Tác giả	Verbalearn
Số trang	31
Lời giải chi tiết	Có

Mục lục tài liệu

Nguyên hàm và tính chất
Tính nguyên hàm bằng phương pháp đổi biến số
Phương pháp tính nguyên hàm từng phần
Dạng 1: Tìm nguyên hàm bằng các phép biến đổi sơ cấp
Dạng 2: Phương pháp đổi biến dạng 1, đặt u =u(x)
Dạng 3: Tìm nguyên hàm bằng cách đổi biến dạng 2
Dạng 4: Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần
Dạng 5: Các bài toán thực tế ứng dụng nguyên hàm

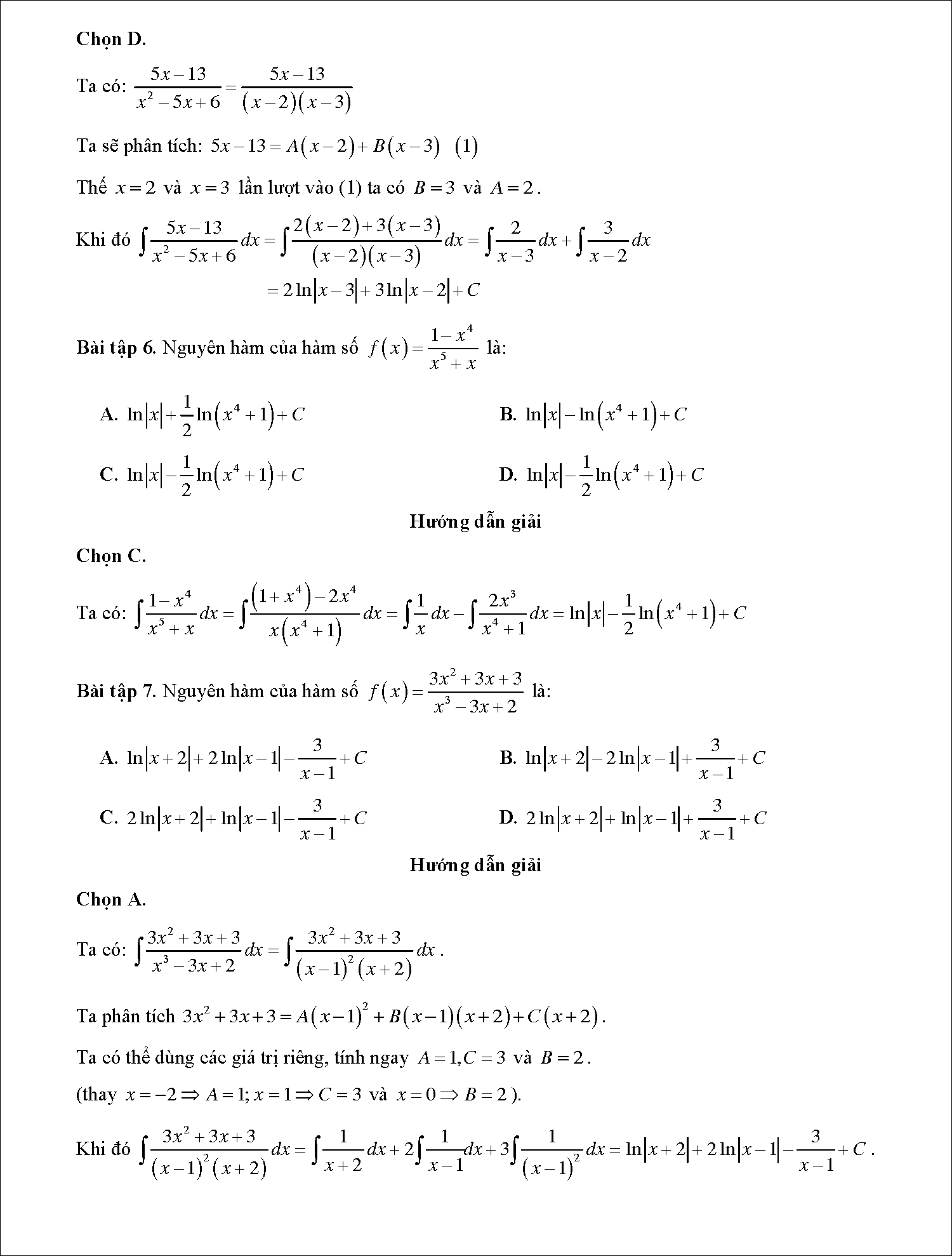
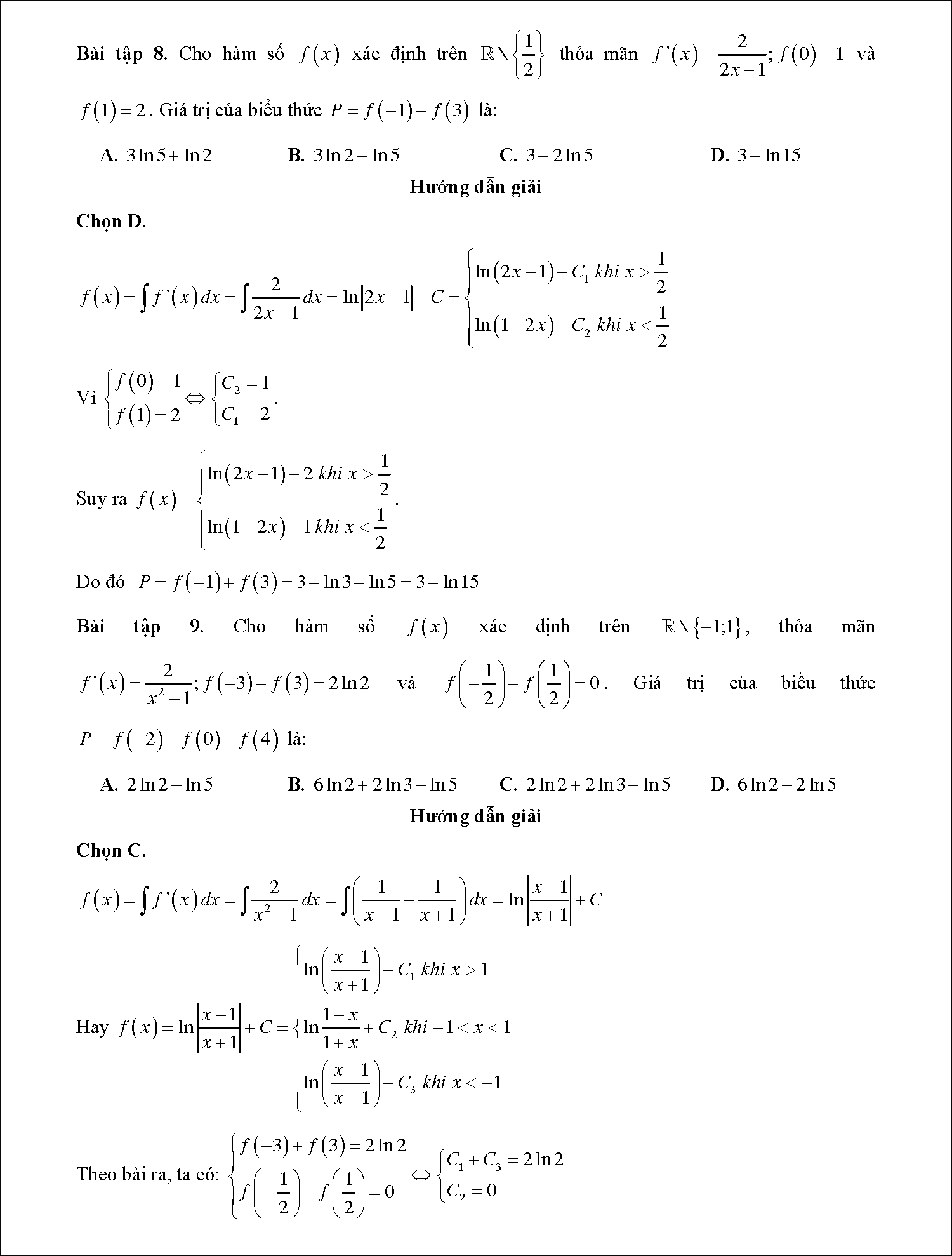
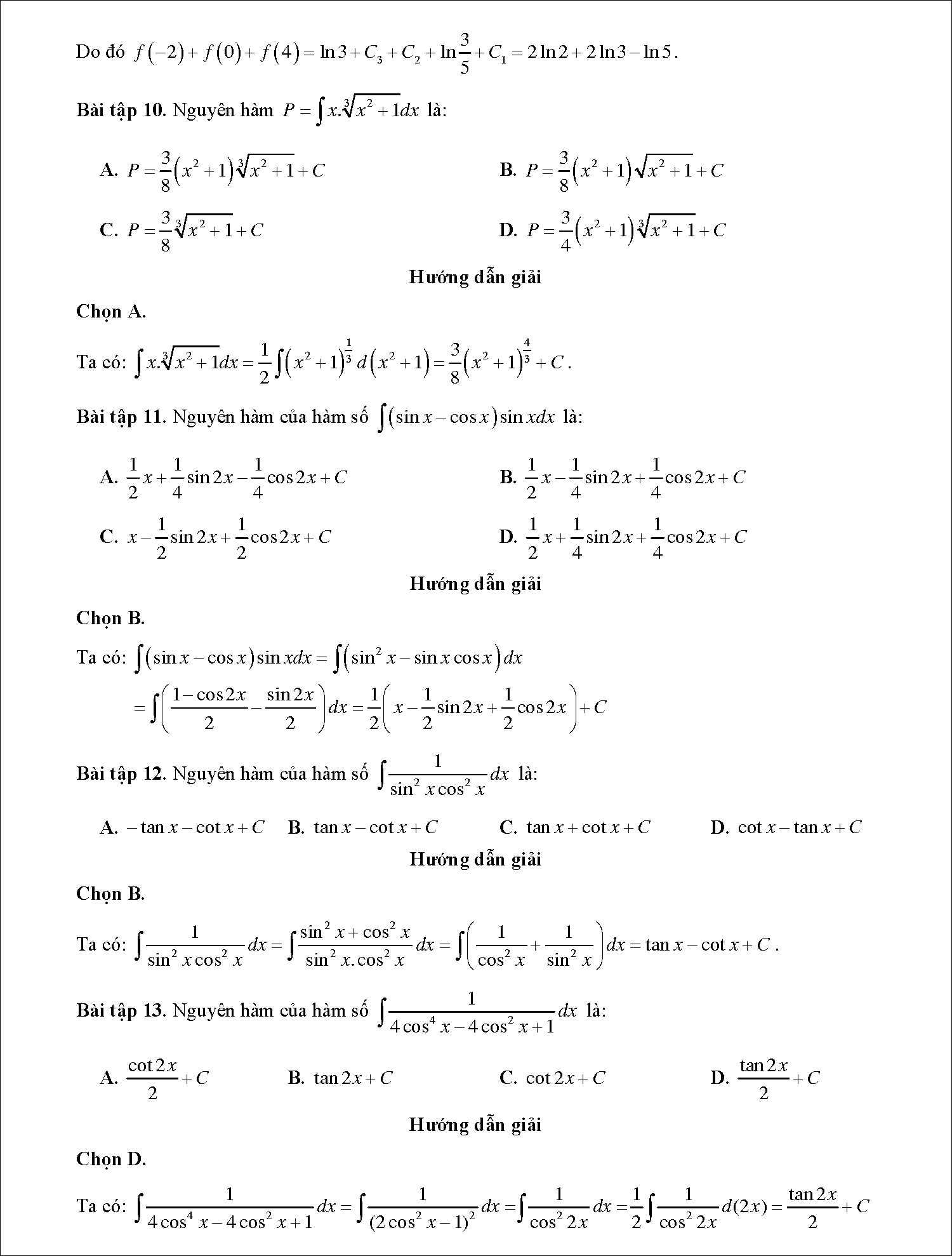
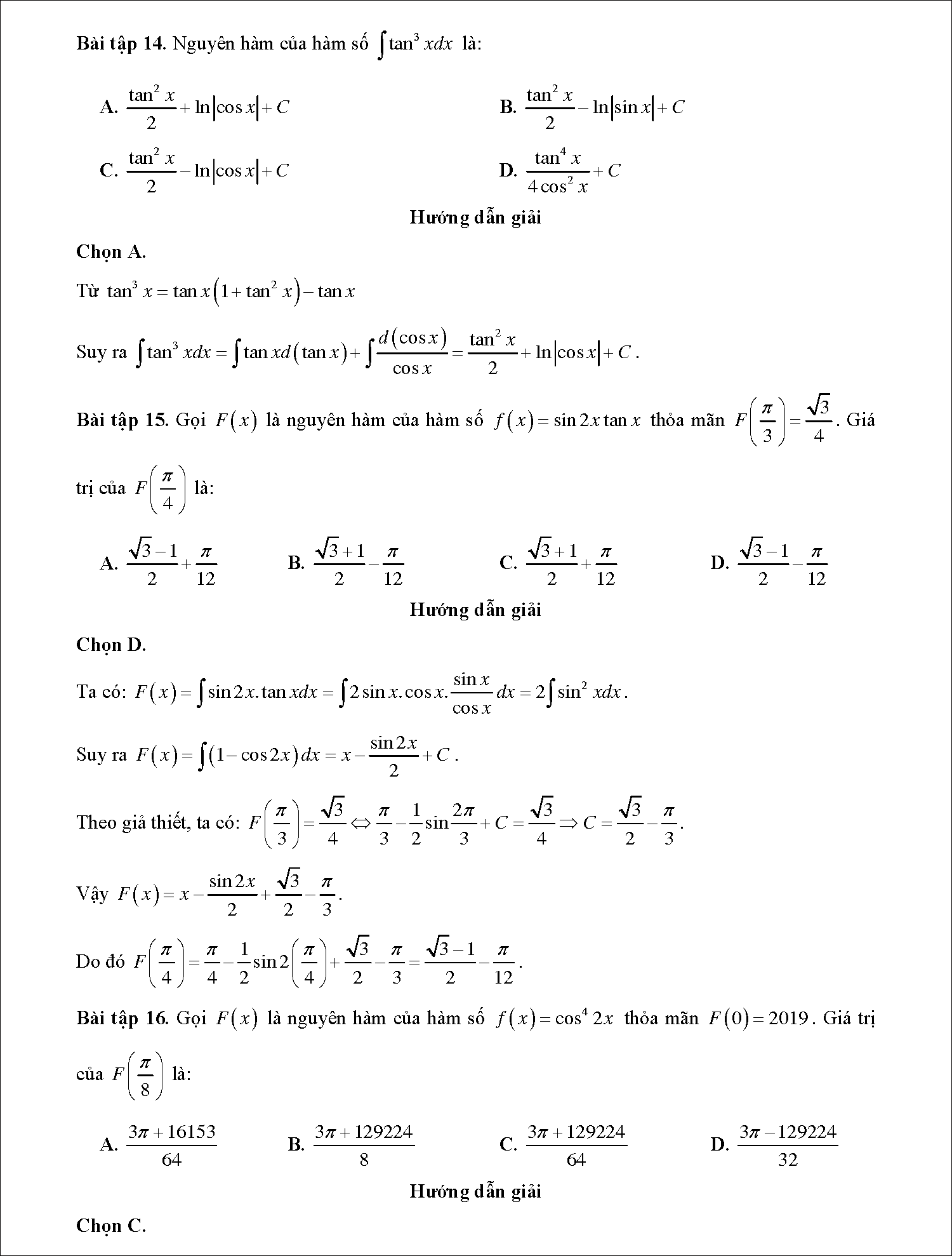
#3. Tính nhanh nguyên hàm – tích phân từng phần sử dụng sơ đồ đường chéo

Thông tin tài liệu
Tác giả	Thầy Ngô Quang Chiến
Số trang	7
Lời giải chi tiết	Có

Mục lục tài liệu

Nhắc lại kiến thức nguyên hàm
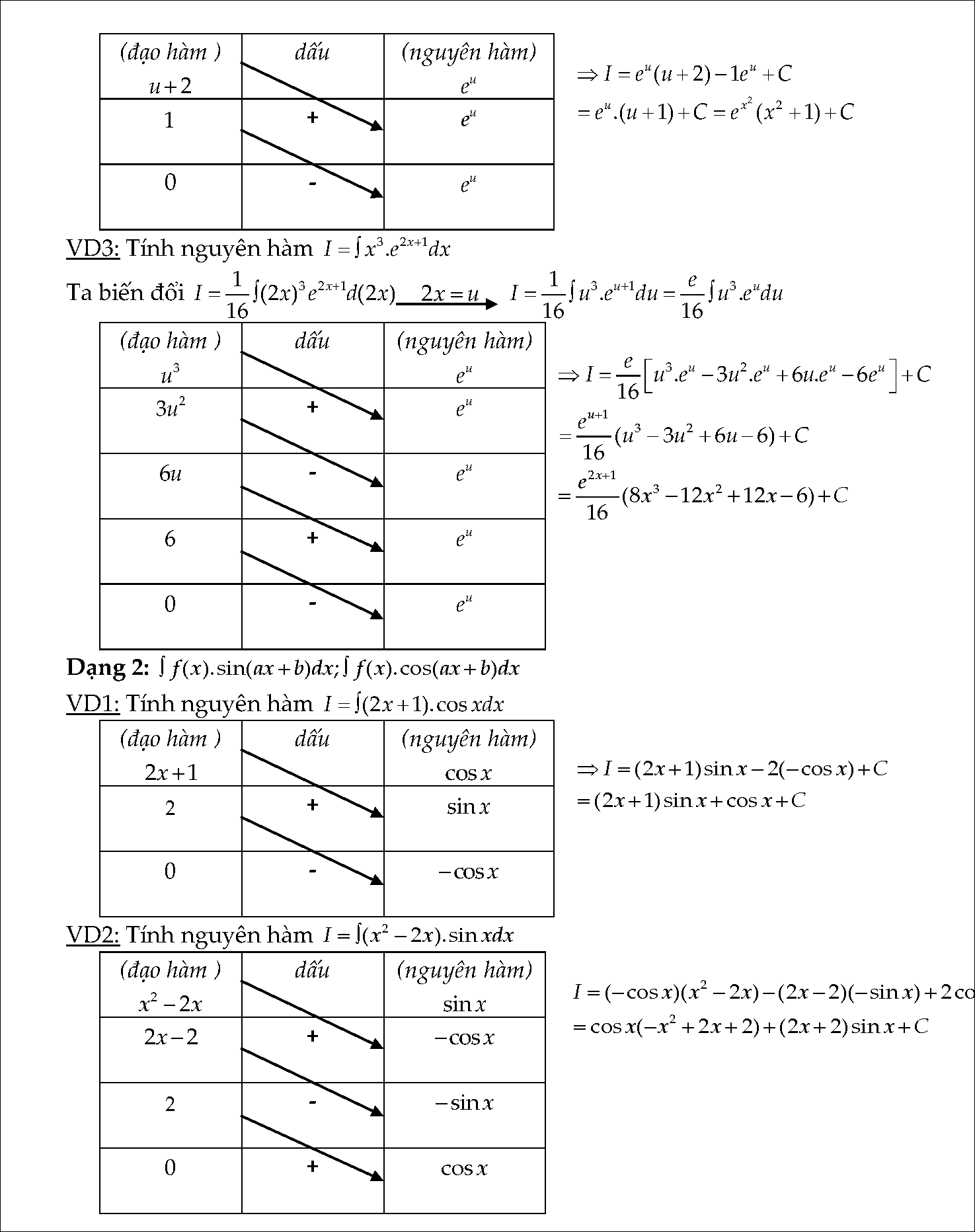
Dạng 1: Tính nguyên hàm của f(x). e^(ax + b)
Dạng 2: Tính nguyên hàm của f (x).sin(ax + b)dx; và nguyên hàm của f (x).cos(ax + b)dx
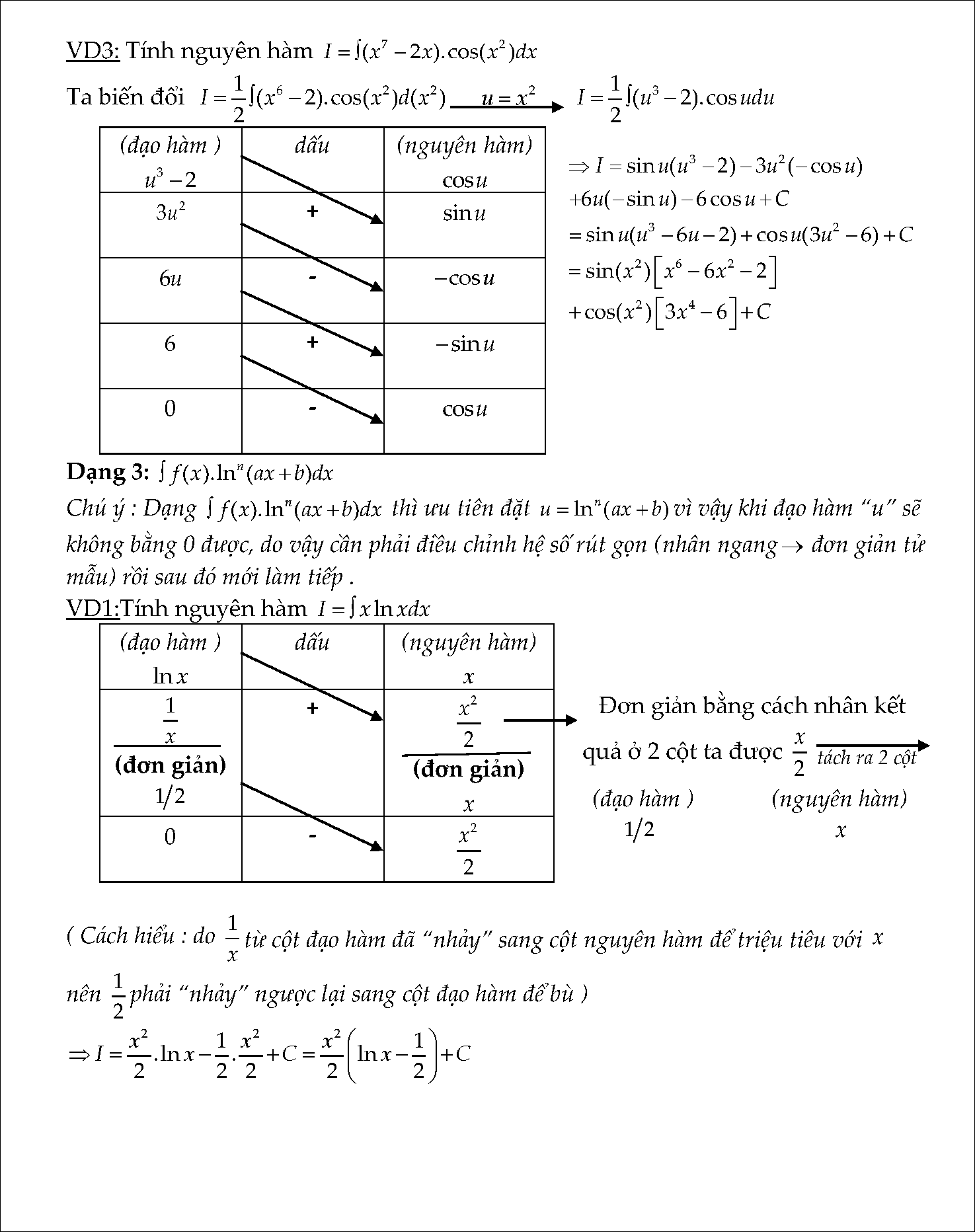
Dạng 3: Tính nguyên hàm của f(x).ln^n(ax+b)dx
Dạng 4: Tính nguyên hàm lặp
Bài tập vận dụng có đáp án

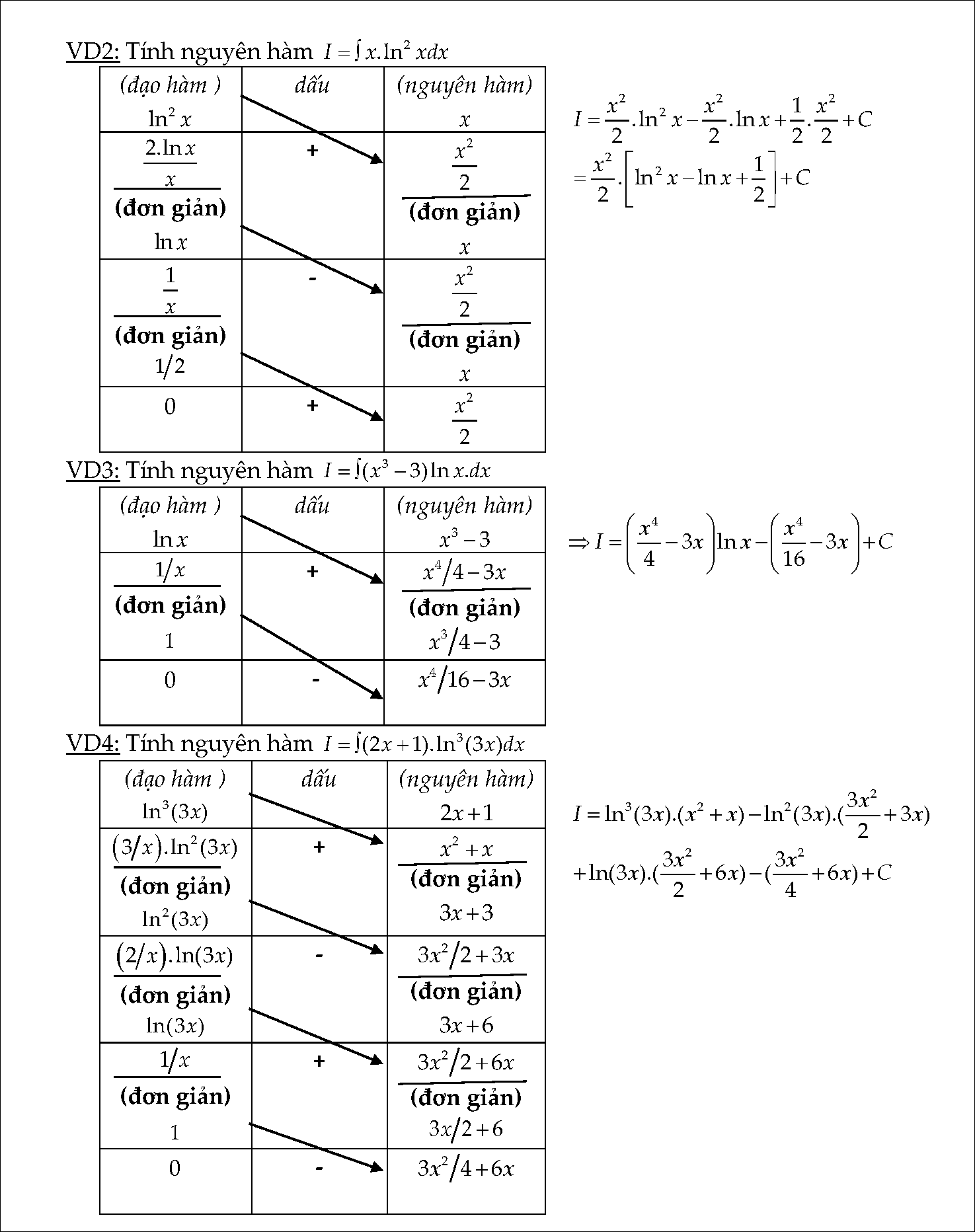
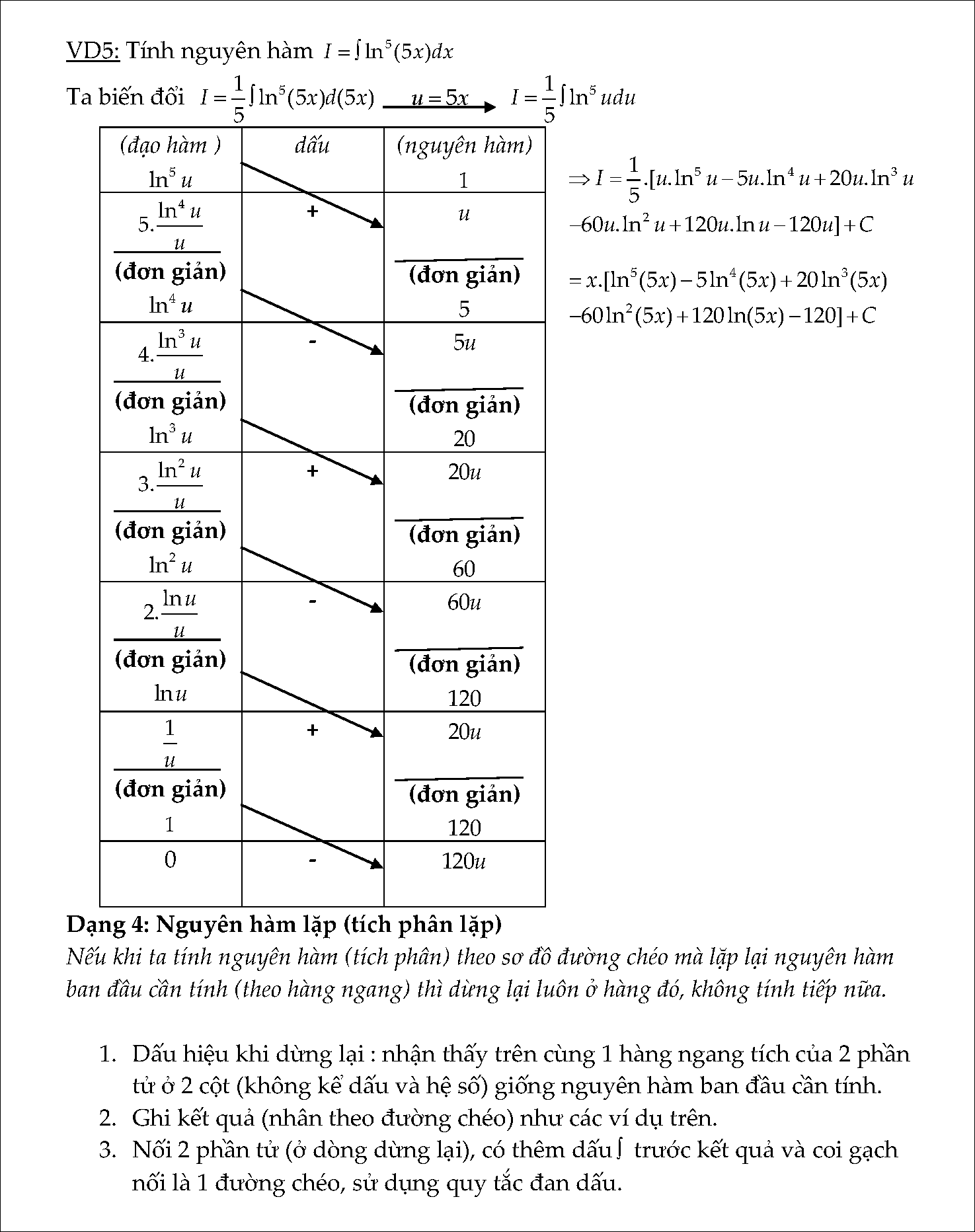
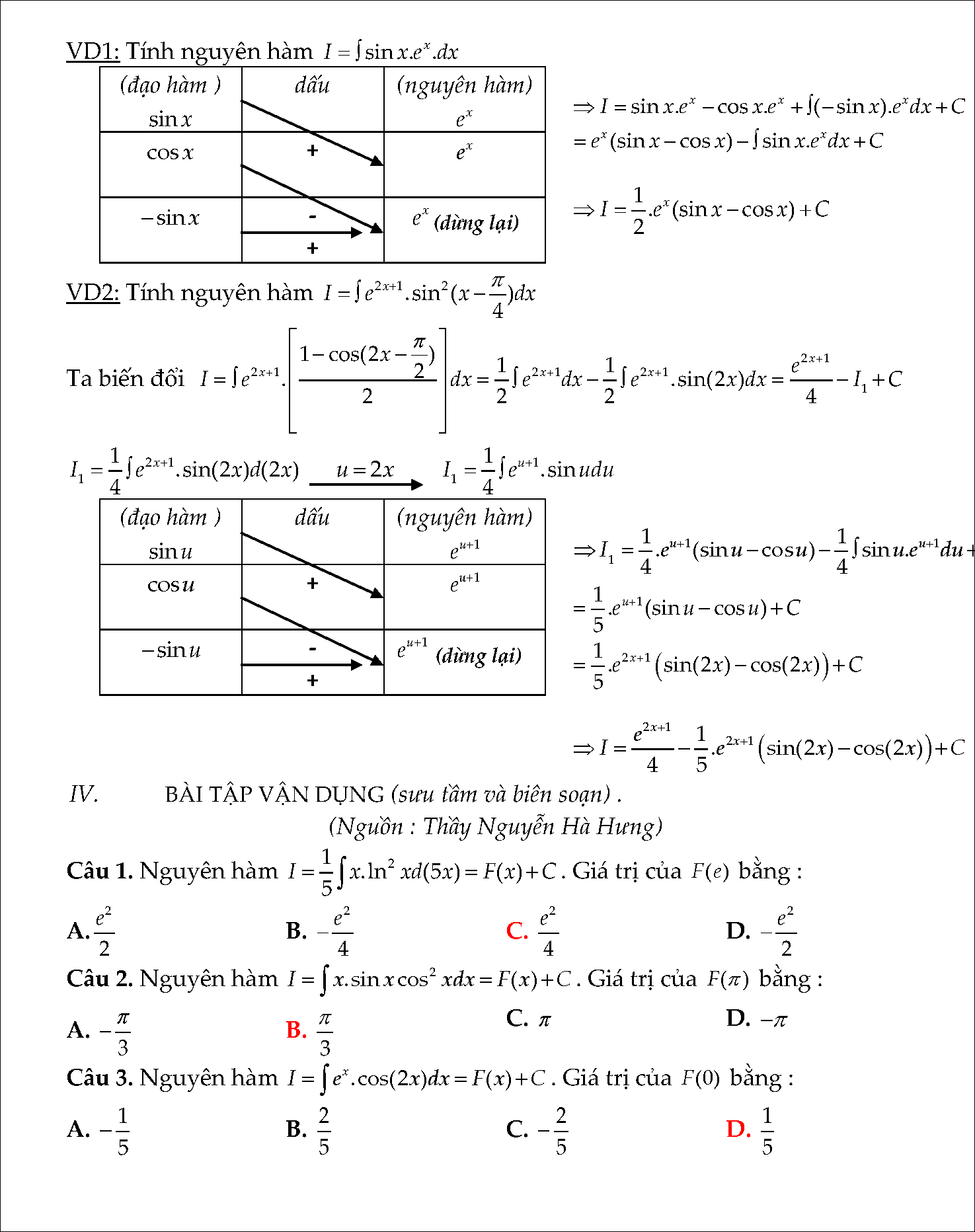
#4. Nguyên hàm và các phương pháp tính nguyên hàm

Thông tin tài liệu
Tác giả	luyenthitracnghiem.vn
Số trang	95
Lời giải chi tiết	Có

Mục lục tài liệu

Dạng 1: Tính nguyên hàm bằng bảng nguyên hàm
Dạng 2: Nguyên hàm của hàm số hữu tỉ (Phân số không căn)
Dạng 3: Nguyên hàm từng phần
Dạng 4: Nguyên hàm đổi biến số
Dạng 5: Tính chất nguyên hàm & nguyên hàm của hàm ẩn

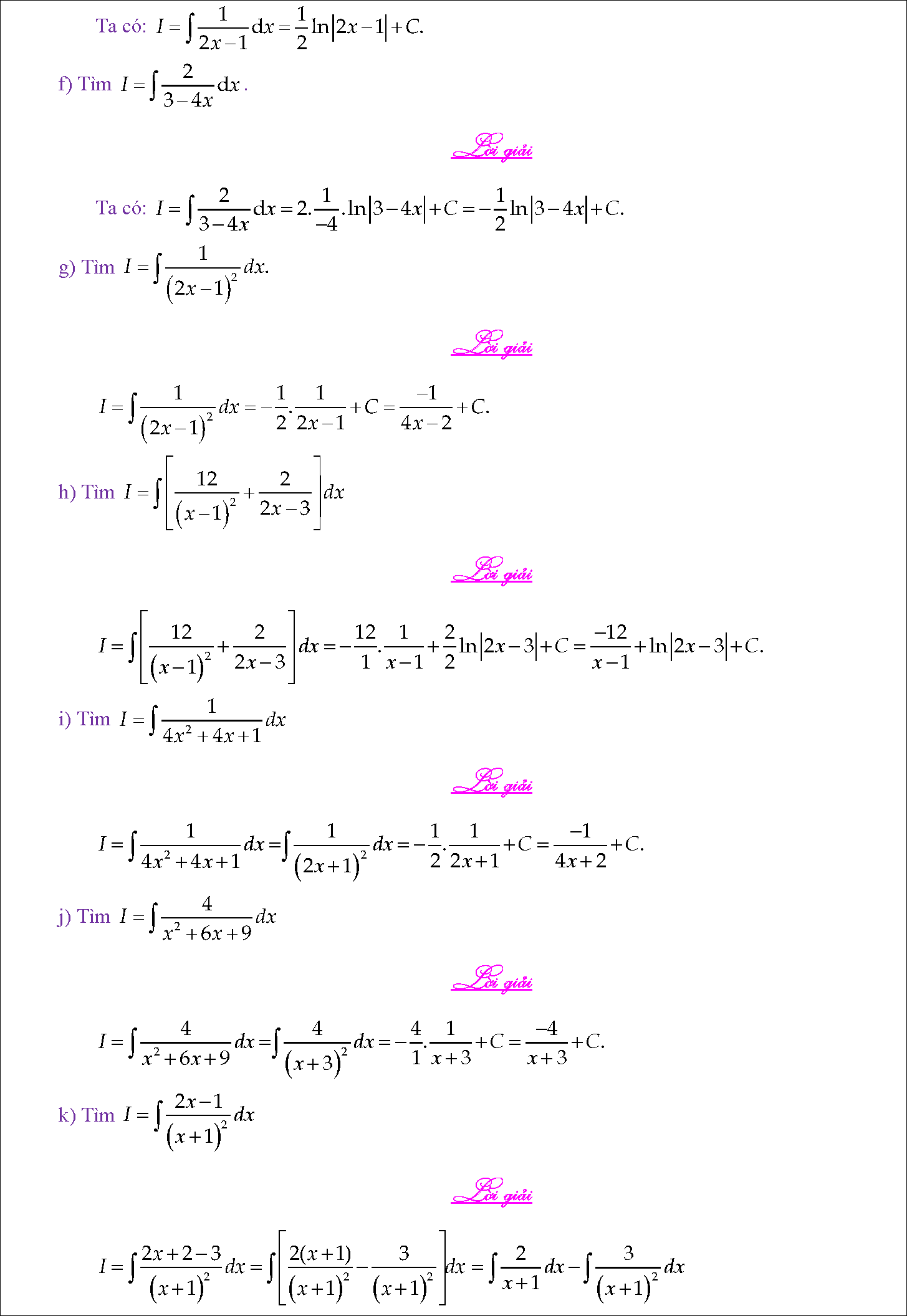
#5. Cách bấm máy tính nguyên hàm

Thông tin tài liệu
Tác giả	Verbalearn
Số trang	5
Lời giải chi tiết	Có

Mục lục tài liệu

Dạng 1: Tìm nguyên hàm F(x) của hàm số f(x)
Dạng 2: Tìm 1 nguyên hàm F(x) của hàm số f(x), biết F(xo) = M
Dạng 3: Tính tích phân khi các đáp án đều là số vô tỷ: căn thức, e, pi
Dạng 4: Ứng dụng tính diện tích hình phẳng, thế tích khối tròn xoay

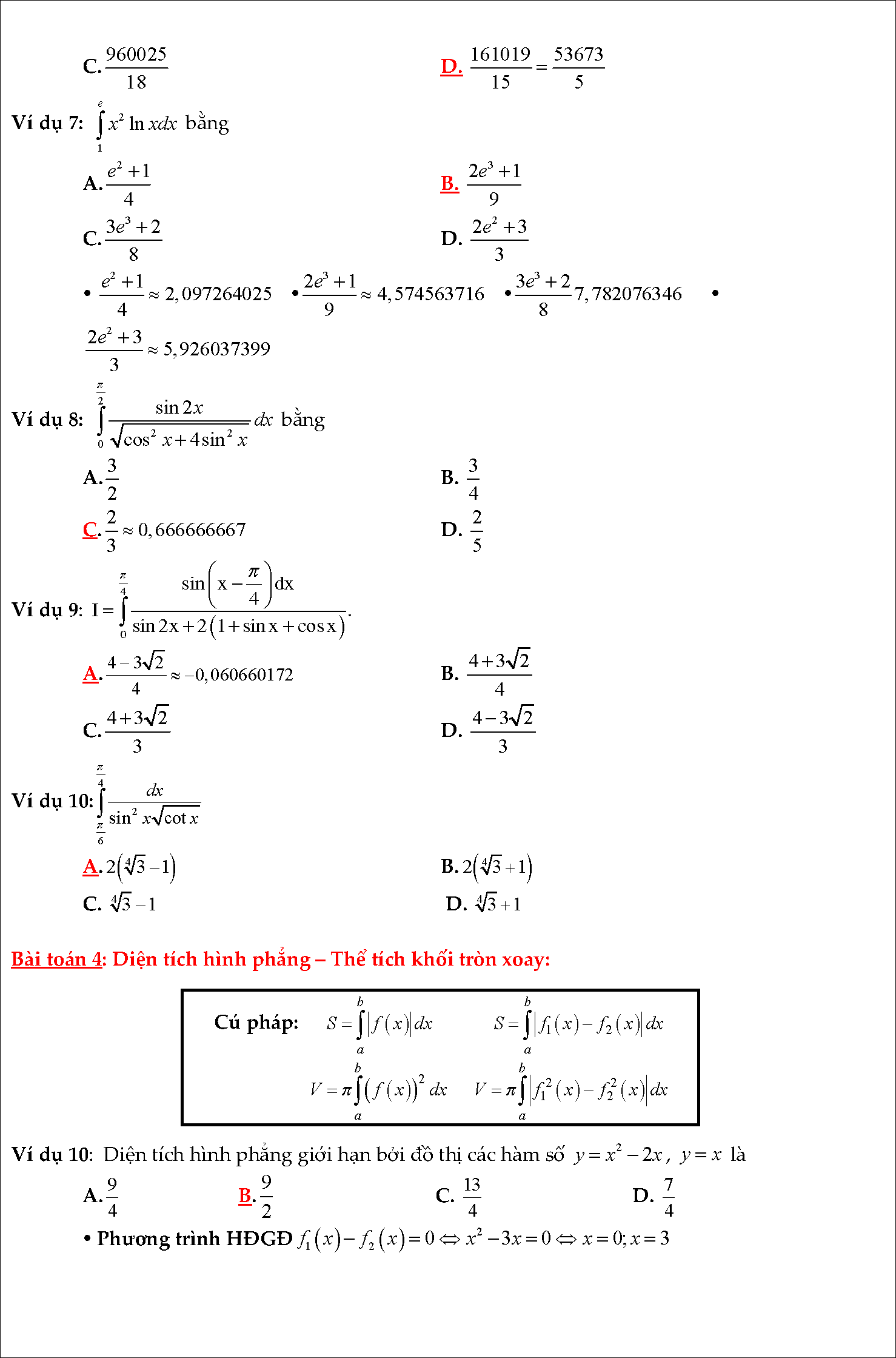
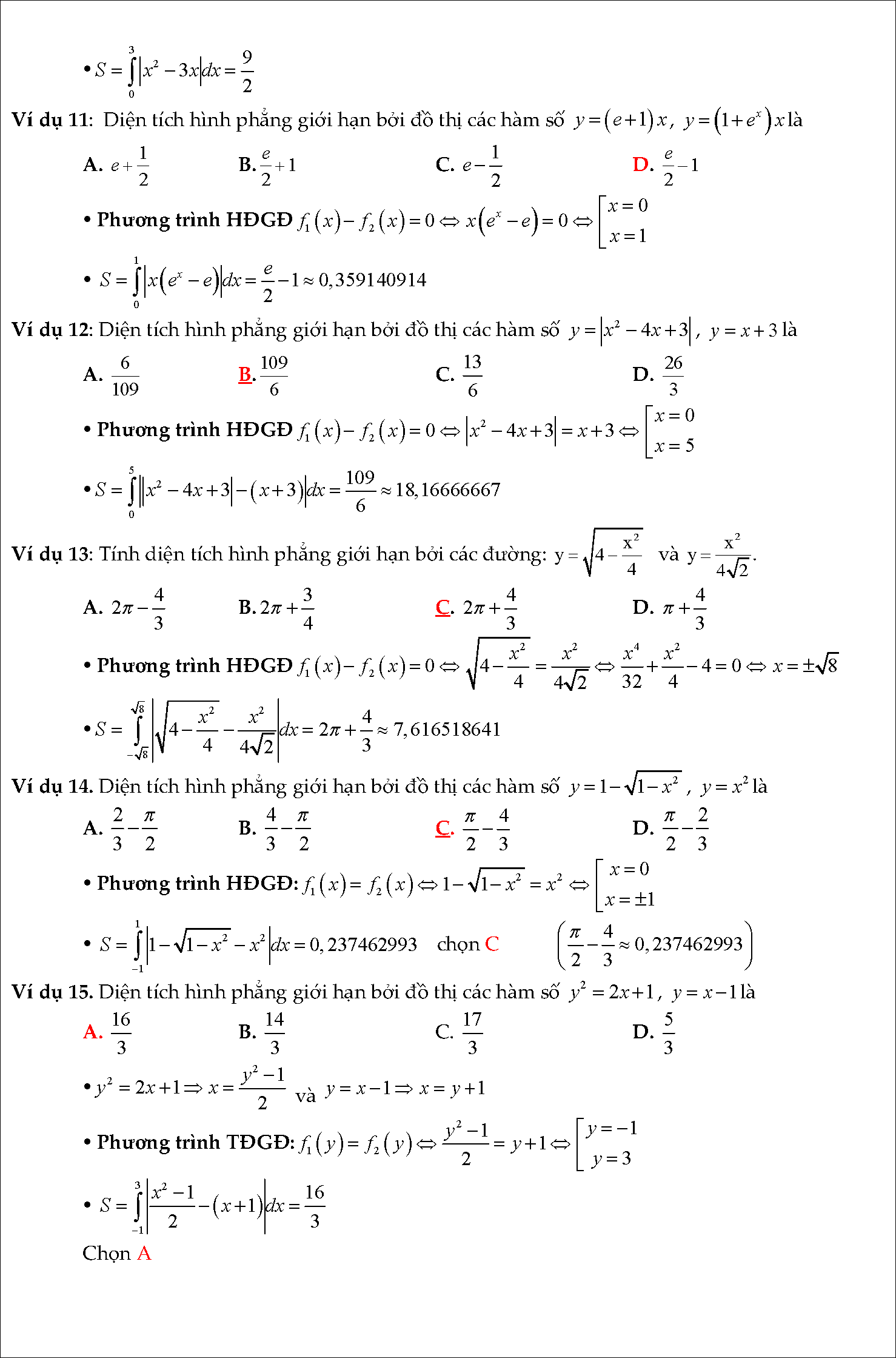
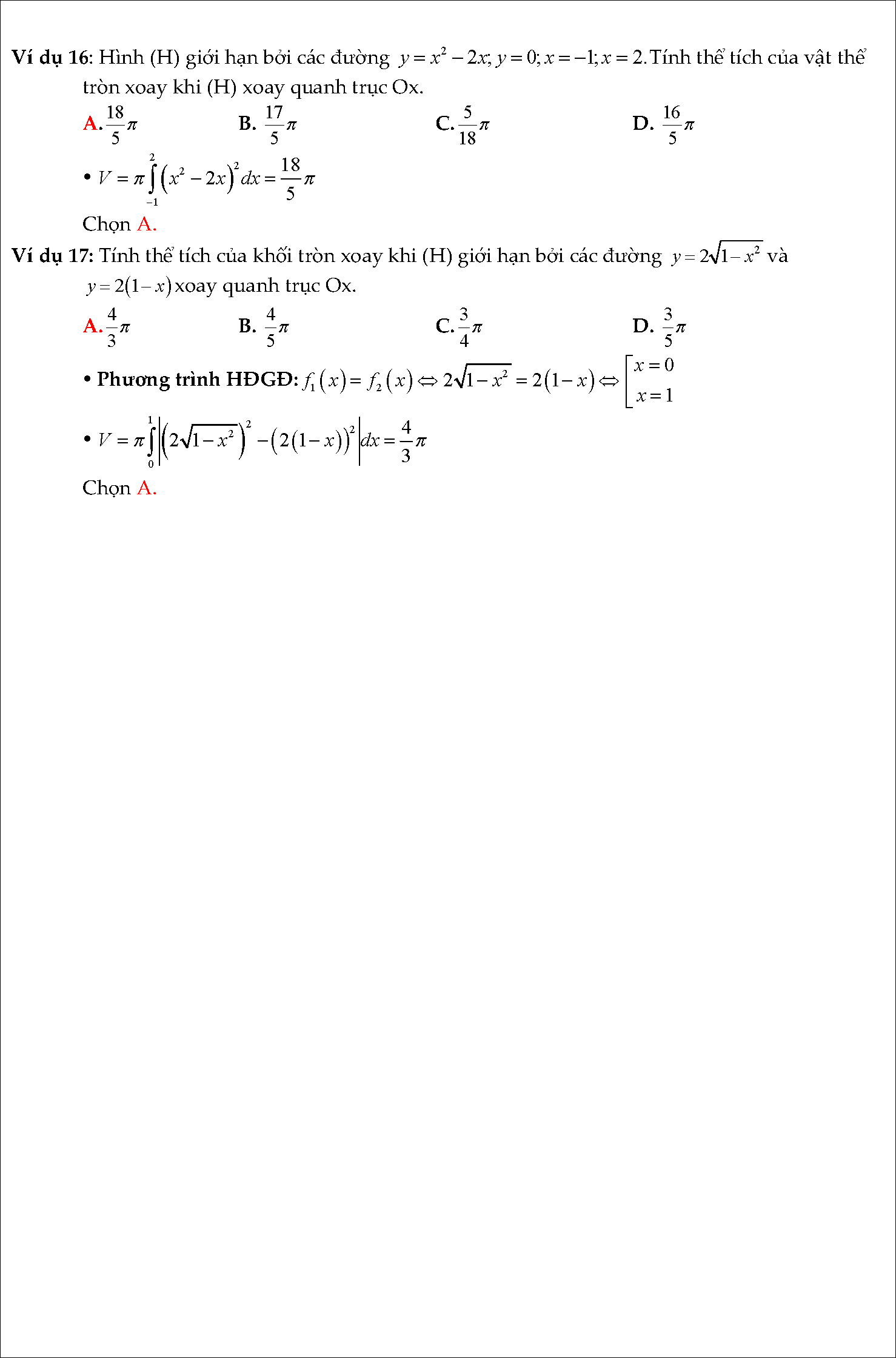
#6. Tóm tắt lý thuyết và bài tập trắc nghiệm nguyên hàm

Thông tin tài liệu
Tác giả	Verbalearn
Số trang	33
Lời giải chi tiết	Có

Mục lục tài liệu

Nguyên hàm và các tính chất
Phương pháp đổi biến số
Phương pháp nguyên hàm từng phần
Bài tập trắc nghiệm
Nguyên hàm của hàm số lượng giác
Nguyên hàm của hàm số mũ, logarit
Nguyên hàm của hàm số chứa căn thức

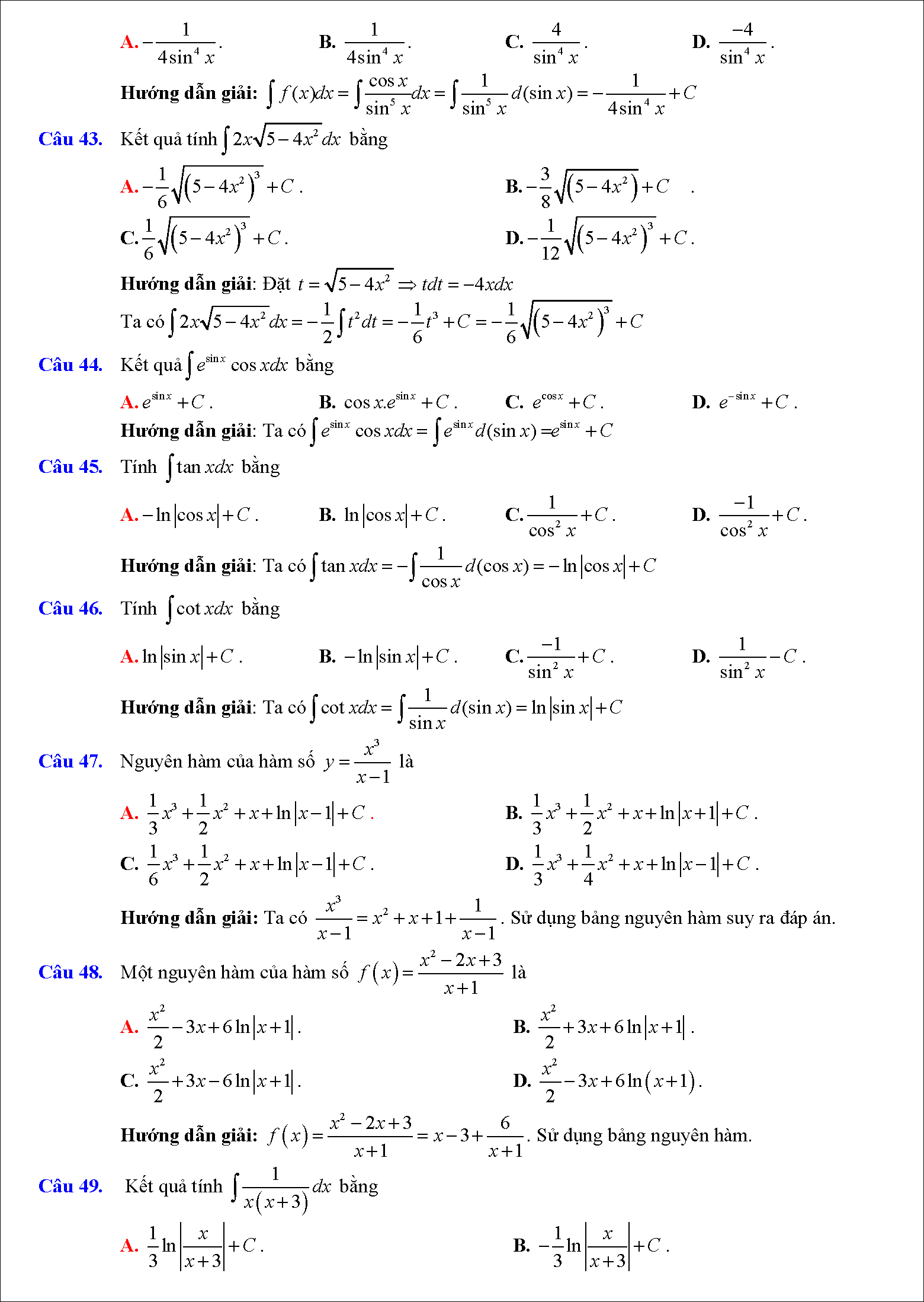
#7. Tổng ôn tập TN THPT 2020 Nguyên Hàm

Thông tin tài liệu
Tác giả	Thầy Nguyễn Bảo Vương
Số trang	38
Lời giải chi tiết	Có

Mục lục tài liệu

Nguyên hàm cơ bản
Nguyên hàm của hàm số hữu tỉ
Tính nguyên hàm bằng phương pháp từng phần
Nguyên hàm có điều kiện
Nguyên hàm hàm ẩn
Đáp án và lời giải chi tiết

#8. Nguyên hàm – tích phân và ứng dụng trong các đề thi thử THPT QG môn Toán

Thông tin tài liệu
Tác giả	GeoGebraPro
Số trang	393
Lời giải chi tiết	Có

Mục lục tài liệu

Tổng hợp các câu nguyên hàm – tích phân trong các đề thi thử THPT QG môn Toán
Các câu hỏi đều có đáp án và lời giải chuẩn từ BGD & ĐT

Xem thêm: Khám phá ngay cách tải video ngắn trên Facebook về điện thoại chỉ trong vài bước

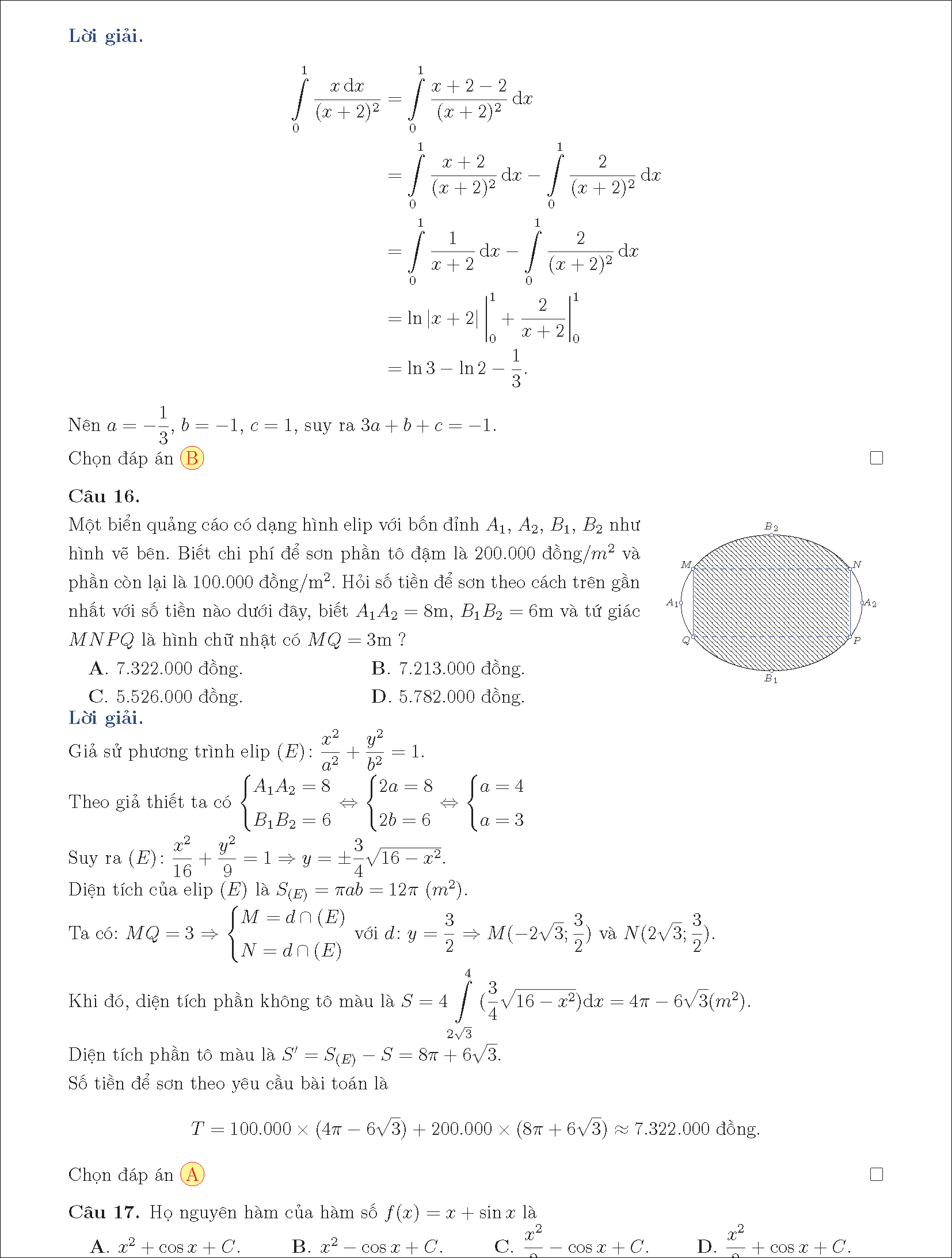
Thầy Dũng dạy toán học từ năm 2010 sau khi nhận bằng sư phạm môn toán tại trường Đại Học Sư Phạm Đà Nẵng. Triết lý dạy học của thầy luôn coi trọng chất lượng hơn số lượng bởi ở một góc nhìn nào đó, tất cả chúng ta sử dụng toán học hằng ngày trong đời sống và cần phải hiểu rõ về thực chất của nó thay vì học sơ sài. Thầy cảm xúc rất suôn sẻ khi được làm biên tập viên cho môn toán tại VerbaLearn, nơi mà những bài dạy của thầy hoàn toàn có thể tiếp cận nhiều học viên hơn .

Source: https://taimienphi.club
Category: Chưa phân loại