Lý thuyết các hệ thức lượng trong tam giác và giải tam giác>

Nhắc lại hệ thức lượng trong tam giác vuông .Cho tam giác \ ( ABC \ ) vuông góc tại đỉnh \ ( A \ ) ( \ ( \ widehat { A } = 90 ^ 0 \ ) ), ta có :1. \ ( { b ^ 2 } = ab ‘ ; { c ^ 2 } = a. c ‘ \ )

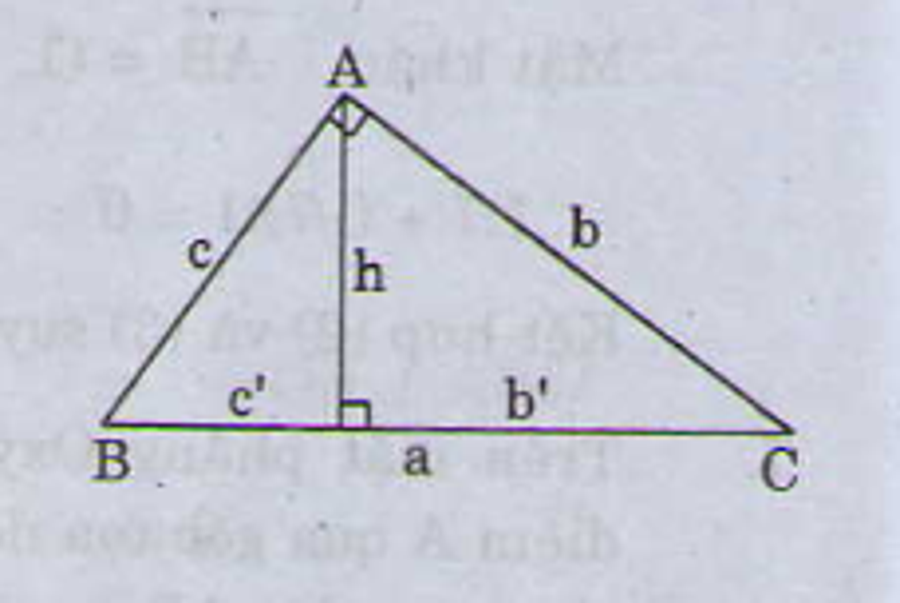
2. Định lý Pitago : \({a^2} = {b^2} + {c^2}\)

3. \ ( a. h = b. c \ )4. \ ( h ^ 2 = b ’. c ’ \ )5. \ ( \ dfrac { 1 } { h ^ { 2 } } \ ) = \ ( \ dfrac { 1 } { b ^ { 2 } } \ ) + \ ( \ dfrac { 1 } { c ^ { 2 } } \ )

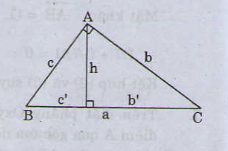
1. Định lý cosin

Định lí : Trong một tam giác bất kỳ, bình phương một cạnh bằng tổng những bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với \ ( cosin \ ) của góc xen giữa chúng .Ta có những hệ thức sau :

$$\eqalign{
& {a^2} = {b^2} + {c^2} – 2bc.\cos A \, \, (1) \cr
& {b^2} = {a^2} + {c^2} – 2ac.\cos B \, \, (2) \cr
& {c^2} = {a^2} + {b^2} – 2ab.\cos C \, \, (3) \cr} $$

\ ( \ cos A = \ dfrac { b ^ { 2 } + c ^ { 2 } – a ^ { 2 } } { 2 bc } \ ) \ ( \ cos B = \ dfrac { a ^ { 2 } + c ^ { 2 } – b ^ { 2 } } { 2 ac } \ )\ ( \ cos C = \ dfrac { a ^ { 2 } + b ^ { 2 } – c ^ { 2 } } { 2 ab } \ )Áp dụng : Tính độ dài đường trung tuyến của tam giác :Cho tam giác \ ( ABC \ ) có những cạnh \ ( BC = a, CA = b \ ) và \ ( AB = c \ ). Gọi \ ( m_a, m_b \ ) và \ ( m_c \ ) là độ dài những đường trung tuyến lần lượt vẽ từ những đỉnh \ ( A, B, C \ ) của tam giác. Ta có\ ( { m_ { a } } ^ { 2 } \ ) = \ ( \ dfrac { 2. ( b ^ { 2 } + c ^ { 2 } ) – a ^ { 2 } } { 4 } \ )\ ( { m_ { b } } ^ { 2 } \ ) = \ ( \ dfrac { 2. ( a ^ { 2 } + c ^ { 2 } ) – b ^ { 2 } } { 4 } \ )\ ( { m_ { c } } ^ { 2 } \ ) = \ ( \ dfrac { 2. ( a ^ { 2 } + b ^ { 2 } ) – c ^ { 2 } } { 4 } \ )

2. Định lí sin

Định lí : Trong tam giác \ ( ABC \ ) bất kể, tỉ số giữa một cạnh và sin của góc đối lập với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là\ ( \ dfrac { a } { \ sin A } = \ dfrac { b } { \ sin B } = \ dfrac { c } { \ sin C } = 2R \ )với \ ( R \ ) là nửa đường kính đường tròn ngoại tiếp tam giác

Công thức tính diện tích tam giác

Ta kí hiệu ha, hb và hc là các đường cao của tam giác \(ABC\) lần lượt vẽ từ các đình \(A, B, C\) và \(S\) là diện tích tam giác đó.

Diện tích \ ( S \ ) của tam giác \ ( ABC \ ) được tính theo một trong những công thức sau\ ( S = \ dfrac { 1 } { 2 } ab \ sin C = \ dfrac { 1 } { 2 } bc \ sin A \ ) \ ( = \ dfrac { 1 } { 2 } ca \ sin B \, \, ( 1 ) \ )\ ( S = \ dfrac { abc } { 4R } \, \, ( 2 ) \ )\ ( S = pr \, \, ( 3 ) \ )\ ( S = \ sqrt { p ( p – a ) ( p – b ) ( p – c ) } \ ) ( công thức Hê – rông ) \ ( ( 4 ) \ )

3. Giải tam giác và ứng dụng vào việc đo đạc

Giải tam giác : Giải tam giác là tìm một số ít yếu tố của tam giác khi đã biết những yếu tố khác của tam giác đó .Muốn giải tam giác ta cần tìm mối liên hệ giữa những yếu tố đã cho với những yếu tố chưa biết của tam giác trải qua những hệ thức đã được nêu trong định lí cosin, định lí sin và những công thức tính diện tích quy hoạnh tam giác .

Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:

a ) Giải tam giác khi biết một cạnh và hai góc .Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lạib ) Giải tam giác khi biết hai cạnh và góc xen giữaĐối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ bac ) Giải tam giác khi biết ba cạnhĐối với bài toán này ta sử dụng định lí cosin để tính góc\ ( \ cos A = \ dfrac { b ^ { 2 } + c ^ { 2 } – a ^ { 2 } } { 2 bc } \ )\ ( \ cos B = \ dfrac { a ^ { 2 } + c ^ { 2 } – b ^ { 2 } } { 2 ac } \ )\ ( cos C = \ dfrac { a ^ { 2 } + b ^ { 2 } – c ^ { 2 } } { 2 ab } \ )

Chú ý: 

1. Cần lưu ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2)

2. Việc giải tam giác được sử dụng vào những bài toán thực tiễn, nhất là những bài toán đo đạc .

Source: https://taimienphi.club
Category: Chưa phân loại