Hình tam giác là gì?
Tam giác hay hình tam giác là một mô hình cơ bản trong hình học : hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối những đỉnh với nhau. Tam giác là đa giác có số cạnh tối thiểu ( 3 cạnh ). Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi ( những góc trong luôn nhỏ hơn 180 o ).
Các loại tam giác
Tam giác thường: là tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác.
Tam giác cân: là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.
Bạn đang xem : Công thức tính diện tích tam giác
Tam giác đều: là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng 60.

Tam giác vuông: là tam giác có một góc bằng 90 (là góc vuông).
Tam giác tù: là tam giác có một góc trong lớn hơn lớn hơn 90(một góc tù) hay có một góc ngoài bé hơn 90 (một góc nhọn).
Tam giác nhọn: là tam giác có ba góc trong đều nhỏ hơn 90 (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 90 (sáu góc tù).

Tam giác vuông cân: vừa là tam giác vuông, vừa là tam giác cân.

Công thức tính diện tích tam giác: vuông, thường, cân, đều
Tính diện tích tam giác thường
Tam giác thường là tam giác có độ dài ba cạnh khác nhau và số đo ba góc cũng không bằng nhau .
Tam giác thường hoàn toàn có thể gồm có những trường hợp đặc biệt quan trọng khác như tam giác cân, tam giác vuông, tam giác đều. Vì thế, hoàn toàn có thể vận dụng cùng những công thức dưới đây để tính diện tích cho nhiều tam giác khác nhau .
+ Tính diện tích khi biết độ dài đường cao
Diện tích tam giác bằng ½ tích đường cao hạ từ đỉnh nhân với cạnh đối lập của đỉnh đó .

Tam giác ABC có ba cạnh a, b, c, ha là đường cao từ đỉnh A như hình vẽ :

Công thức chung
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối lập của đỉnh đó .

Tính diện tích tam giác khi biết một góc
Ví dụ: Tính diện tích tam giác ABC có độ dài cạnh đáy là 32cm và chiều cao là 22cm.

Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác .

Ví dụ: Cho tam giác ABC có góc B bằng 60 độ, cạnh BC = 7, cạnh AB = 5. Tính diện tích tam giác ABC?

Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
Sử dụng công thức Heron đã được chứng tỏ :

Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
p: Nửa chu vi tam giác, bằng ½ tổng các cạnh của một tam giác.
Với p là nửa chu vi tam giác :

Có thể viết lại bằng công thức :

Ví dụ: Tính diện tích hình tam giác có độ dài cạnh AB = 8, AC = 7, CB = 9

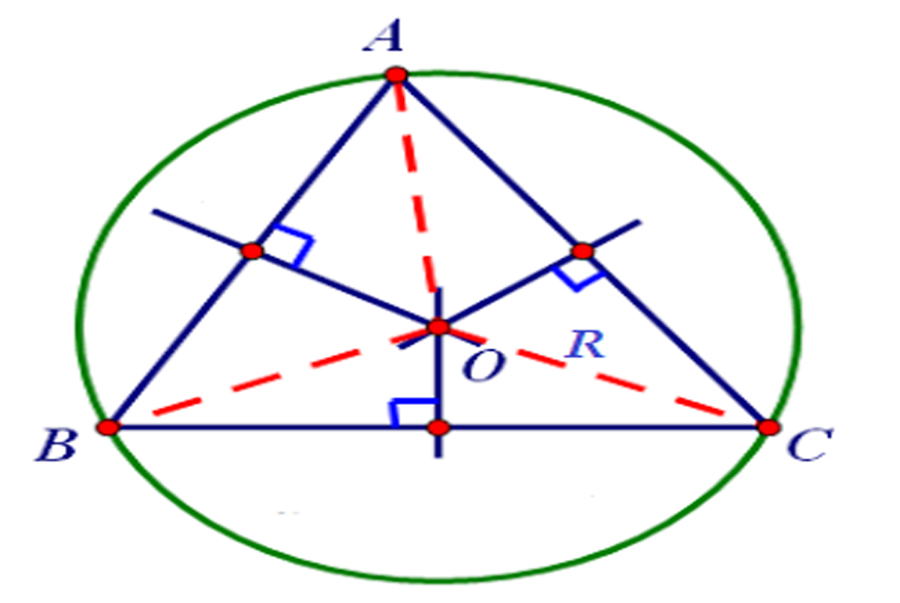
Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R)

Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
R: Bán kính đường tròn ngoại tiếp.

Gọi R là nửa đường kính đường tròn ngoại tiếp tam giác ABC .
Ta có :

Cách khác :
Lưu ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.
Ví dụ: Cho tam giác ABC, độ dài các cạnh a = 6, b = 7, c = 5, R = 3 (R là bán kính đường tròn ngoại tiếp tam giác ABC).

Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r)

Trong đó:
p: Nửa chu vi tam giác.
r: Bán kính đường tròn nội tiếp.

Gọi r là nửa đường kính đường tròn nội tiếp tam giác ABC và p là nửa chu vi tam giác p = ( a + b + c ) / 2 .
Ví dụ: Tính diện tích tam giác ABC biết độ dài các cạnh AB = 20, AC = 21, BC = 15, r = 5 (r là bán kính đường tròn nội tiếp tam giác ABC).

Các công thức tính diện tích tam giác trong không gian
Trong mặt phẳng Oxy, gọi tọa độ những đỉnh của tam giác ABC lần lượt là : A ( xA, yA ), B ( xB, yB ), C ( xC, yC ), ta hoàn toàn có thể sử dụng những công thức sau để tính diện tích tam giác

Trong mặt phẳng Oxy, gọi tọa độ những đỉnh của tam giác ABC là :

Áp dụng trong không gian, với khái niệm tích có hướng của 2 vectơ. Ta có:

Ví dụ: Trong không gian Oxyz cho 3 điểm A(1;2;1), B(2;-1;3), C(5;2;-3). Tính diện tích của tam giác ABC.

Bài tập ví dụ
* Tính diện tích hình tam giác có
a, Độ dài đáy là 15 cm và chiều cao là 12 cm
b, Độ dài đáy là 6 m và chiều cao là 4,5 m
Lời giải:
a, Diện tích của hình tam giác là :
( 15 x 12 ) : 2 = 90 ( cm2 )
Đáp số : 90 cm2
b, Diện tích của hình tam giác là :
( 6 x 4,5 ) : 2 = 13,5 ( mét vuông )
Đáp số : 13,5 mét vuông
* Chú ý: Trường hợp không cho cạnh đáy hoặc chiều cao, mà cho trước diện tích và cạnh còn lại, các bạn hãy áp dụng công thức suy ra ở trên để tính toán.
Một số chú ý khi tính diện tích tam giác.
– Với tam giác có chứa góc bẹt chiều cao nằm bên ngoài tam giác khi đó độ dài cạnh để tính diện tích chính bằng độ dài cạnh trong tam giác .
– Khi tính diện tích tam giác chiều cao nào ứng với đáy đó .
– Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau -> diện tích hai tam giác tỉ lệ với 2 cạnh đáy và ngược lại nếu hai tam giác có chung đáy ( hoặc hai đáy bằng nhau ) -> diện tích tam giác tỉ lệ với 2 đường cao tương ứng .
Tính diện tích tam giác cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau và số đo hai góc ở đáy cũng bằng nhau .
Tam giác cân ABC có ba cạnh, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, ha là đường cao từ đỉnh A như hình vẽ :

Áp dụng công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân :

Bài tập ví dụ
* Tính diện tích của tam giác cân có :
a, Độ dài cạnh đáy bằng 6 cm và đường cao bằng 7 cm
b, Độ dài cạnh đáy bằng 5 m và đường cao bằng 3,2 m
Lời giải:
a, Diện tích của hình tam giác là :
( 6 x 7 ) : 2 = 21 ( cm2 )
Đáp số : 21 cm2
b, Diện tích của hình tam giác là :
(5 x 3,2) : 2 = 8 (m2)
Đáp số : 8 mét vuông
Tính diện tích tam giác đều
Tam giác đều là tam giác có độ dài ba cạnh bằng nhau, số đo những góc cũng bằng nhau và bằng 60 độ .
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài những cạnh như hình vẽ :

Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích tam giác đều :

Trong đó:
a: Độ dài các cạnh của tam giác đều.
Ví dụ dưới đây sẽ giúp bạn hiểu hơn về công thức tính diện tích tam giác đều bên trên .
Ví dụ: Tính diện tích tam giác đều ABC, cạnh bằng 10.

Bài tập ví dụ
* Tính diện tích của tam giác đều có :
a, Độ dài một cạnh tam giác bằng 6 cm và đường cao bằng 10 cm
b, Độ dài một cạnh tam giác bằng 4 cm và đường cao bằng 5 cm
Lời giải
a, Diện tích hình tam giác là :
( 6 x 10 ) : 2 = 30 ( cm2 )
Đáp số : 30 cm2
b, Diện tích hình tam giác là :
( 4 x 5 ) : 2 = 10 ( cm2 )
Đáp số : 10 cm2
Tính diện tích tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ ( góc vuông ) .
– Công thức tính diện tích tam giác vuông
Ví dụ tam giác ABC vuông tại A. Áp dụng công thức tính diện tích tam giác thường để tính, ta có :

Trong đó:
A, B, C: Các đỉnh của tam giác.
a, b, c: Lần lượt kí hiệu cho độ dài các cạnh BC, AC, AB.
ha: Đường cao hạ từ đỉnh A tương ứng.
S: Diện tích của hình tam giác.
Tam giác ABC vuông tại B, a, b là độ dài hai cạnh góc vuông :

Áp dụng công thức tính diện tích thường cho diện tích tam giác vuông với chiều cao là 1 trong 2 cạnh góc vuông và cạnh đáy là cạnh còn lại .
Công thức tính diện tích tam giác vuông :

Ví dụ: Tính diện tích hình tam giác ABC có độ dài đáy là 32cm và chiều cao là 22cm.

Bài tập ví dụ
* Tính diện tích của tam giác vuông có :
a, Hai cạnh góc vuông lần lượt là 3 cm và 4 cm
b, Hai cạnh góc vuông lần lượt là 6 m và 8 m
Lời giải:
a, Diện tích của hình tam giác là :
( 3 x 4 ) : 2 = 6 ( cm2 )
Đáp số : 6 cm2
b, Diện tích của hình tam giác là :
( 6 x 8 ) : 2 = 24 ( mét vuông )
Đáp số : 24 mét vuông
Tương tự nếu tài liệu hỏi ngược về cách tính độ dài, những bạn hoàn toàn có thể sử dụng công thức suy ra ở trên .
Tính diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông :

Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với độ cao và cạnh đáy bằng nhau, ta có công thức :

Bài tập tự luyện về hình tam giác lớp 5
Bài 1: Tính diện tích hình tam giác MDC (hình vẽ dưới). Biết hình chữ nhật ABCD có AB = 20 cm, BC = 15cm.

Bài 2: Tính chiều cao AH của hình tam giác ABC vuông tại A. Biết : AB = 60 cm ; AC = 80 cm ; BC = 100 cm.
Bài 3: Một hình tam giác có đáy dài 16cm, chiều cao bằng 3/4 độ dài đáy. Tính diện tích hình tam giác đó
Bài 4: Một miếng đát hình tam giác có diện tích 288m2, một cạnh đáy bằng 32m. Hổi để diện tích miếng đát tăng thêm 72m2 thì phải tăng cạnh đáy đã cho thêm bao nhiêu mét?
Bài 5: Chiếc khăn quàng hình tam giác có đáy là 5,6 dm và chiều cao 20cm. Hãy tính diện tích chiếc khăn quàng đó.
Bài 6: Một khu vườn hình tam giác có diện tích 384m2, chiều cao 24m. Hỏi cạnh đáy của tam giác đó là bao nhiêu?
Bài 7: Một cái sân hình tam giác có cạnh đáy là 36m và gấp 3 lần chiều cao. Tính diện tích cái sân hình tam giác đó?
Bài 8: Cho hình tam giác vuông ABC (góc A là góc vuông). Biết độ dài cạnh AC là 12dm, độ dài cạnh AB là 90cm. Hãy tính diện tích hình tam giác ABC?
Bài 9: Cho hình tam giác vuông ABC tại A. Biết AC = 2,2dm, AB = 50cm. Hãy tính diện tích hình tam giác ABC?
Bài 10: Hình tam giác MNP có chiều cao MH = 25cm và có diện tích là 2dm2. Tính độ dài đáy NP của hình tam giác đó?
Bài 11: Một quán ăn lạ có hình dạng là 1 tam giác có tổng cạnh đáy và chiều cao là 24m, cạnh đáy bằng 1515 chiều cao. Tính diện tích quán ăn đó?
Bài 12: Cho tam giác ABC có đáy BC = 2cm. Hỏi phải kéo dài BC thêm bao nhiêu để được tam giác ABD có diện tích gấp rưỡi diện tích tam giác ABC?
Bài 13: Một hình tam giác có cạnh đáy bằng 2/3 chiều cao. Nếu kéo dài cạnh đáy thêm 30dm thì diện tích của hình tam giác tăng thêm 27m2. Tính diện tích hình tam giác đó?
Bài 14: Một hình tam giác có cạnh đáy bằng 7/4 chiều cao. Nếu kéo dài cạnh đáy thêm 5m thì diện tích của hình tam giác tăng thêm 30m2. Tính diện tích hình tam giác đó?
Bài 15: Cho một tam giác ABC vuông ở A. Nếu kéo dài AC về phía C một đoạn CD dài 8cm thì tam giác ABC trở thành tam giác vuông cân ABD và diện tích tăng thêm 144cm2. Tính diện tích tam giác vuông ABC ?
Bài tập về hình tam giác nâng cao
Bài 1: Cho hình tam giác ABC vuông tại A có chu vi bằng 72cm. Độ dài cạnh AB bằng 3/4 độ dài cạnh AC, độ dài cạnh AC bằng 4/5 độ dài cạnh BC. Tính diện tích của tam giác ABC
Bài 2: Trong hình tam giác ABC, biết M và N lần lượt là trung điểm của cạnh AB và AC. Tính diện tích tam giác ABC biết diện tích hình tam giác AMN bằng 5cm2
Bài 3: Cho hình vuông ABCD có AB = 6cm, M là trung điểm của BC, DN = 1/2NC. Tính diện tích hình tam giác AMN.

Bài 4: Cho tam giác MNP. Gọi K là trung điểm của của cạnh NP, I là trung điểm của cạnh MP. Biết diện tích hình tam giác IKP bằng 3,5cm2. Tính diện tích hình tam giác MNP
Bài 5: Cho hình tam giác ABC có cạnh AB dài 20cm, cạnh AC dài 25cm. Trên cạnh AB lấy điểm D cách A 15cm, trên cạnh AC lấy điểm E cách điểm A 20cm. Nối D với E được hình tam giác ADE có diện tích là 45cm2.. Tính diện tích hình tam giác ABC

Bài 6: Cho hình tam giác ABC. Các điểm D, E, G lần lượt là trung điểm của các cạnh AB, BC và AC. Tính diện tích hình tam giác DEG, biết diện tích tam giác ABC là 100m2

Bài 7: (Thi vào 6 trường Archimedes Academy 2019 – 2020 – đợt 2)
Cho tam giác với những tỷ suất như hình .
Biết S3 − S1 = 84 cm2. Tính S4 − S2

Bài 8: (Thi vào 6 trường Hà Nội Amsterdam 2010 – 2011)
Cho tam giác ABC có diện tích là 180 cm2. Biết AB = 3 x BM ; AN = NP = PC ; QB = QC. Tính diện tích tam giác MNPQ ? ( xem hình vẽ )

Bài 9: (Thi vào 6 trường Hà Nội Amsterdam 2006 – 2007)
Cho tam giác ABC có diện tích bằng 18 cm2. Biết DA = 2 x DB ; EC = 3 x EA ; MC = MB ( hình vẽ ). Tính tổng diện tích hai tam giác MDB và MCE ?

Bài 10: (Thi vào 6 trường Hà Nội Amsterdam 2004 – 2005)
Trong hình vẽ bên có NA = 2 x NB; MC = 2 x MB và diện tích tam giác OAN là 8cm2. Tính diện tích BNOM ?

Đăng bởi : trung học phổ thông Sóc Trăng
Chuyên mục : Giáo dục đào tạo
Source: https://taimienphi.club
Category: Chưa phân loại